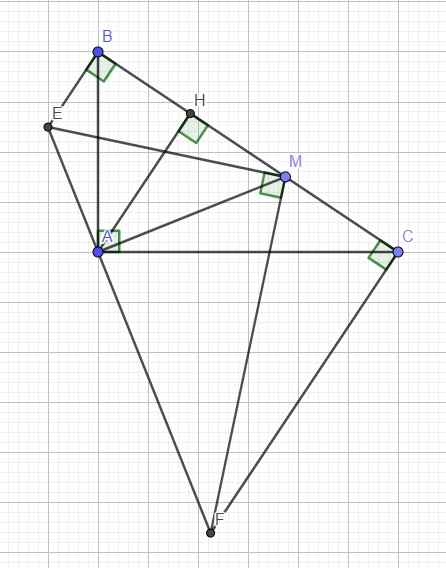
Cho tam giác ABC vuông cân tại A. Trên cùng một nửa mặt phẳng bờ BC chứa A, kẻ các tia Bx, Cy vuông góc với BC. Gọi M là điểm thuộc cạnh BC (M khác B và C). Đường vuông góc với AM tại A cắt Bx, Cy lần lượt tại D và E.
a) Tìm trực tâm của tam giác ABC.
b) Chứng minh rằng: ∆ABM = ∆ACE.
Chứng minh : điểm A cách đều ba đỉnh của tam giác DME
c) Chứng minh : điểm A cách đều ba đỉnh của tam giác DME
d) Tính góc DME.
E) Xác định vị trí của M trên đoạn thẳng BC để DM là phân giác BDE . Tia EM có là tia phân giác của DEC không ? vì sao ?
b) Xác định vị trí của M trên đoạn thẳng BC để DM là phân giác ![]() . Tia EM có là tia phân giác của
. Tia EM có là tia phân giác của ![]() không ? vì sao ?
không ? vì sao ?