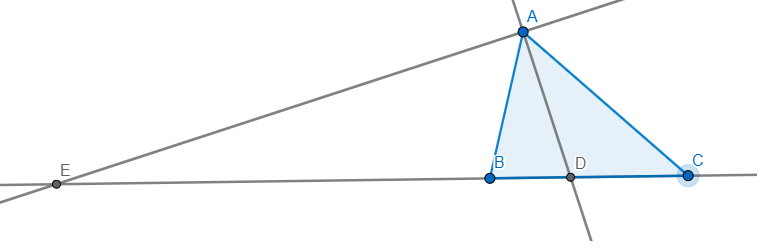
Cho tam giác ABC có CB

CM

Chu Minh Đức

24 tháng 8 2020

Cho tam giác ABC có CB<CA và góc CBA = 90 độ. Điểm D nắm giữa A và C sao cho góc CBD = góc BAC a) chứng minh tam giác ABC đồng dạng tam giác BDC. Suy ra \(BC^2\)=CD.AC b) tia phân giác của góc ACB cắt BA tại E và cắt BD tại F. Chứng minh \(\frac{FD}{FB}\)=\(\frac{EB}{EA}\) c) Đường thẳng vuông góc với CE Tại C cắt đường thẳng AB tại H. chứng minh...

Đọc tiếp

#Toán lớp 8

0

TA

Thu Anh

4 tháng 12 2021

Bài 4: Cho tam giác ABC có góc A = 90 độ . Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. a) Chứng minh tam giác ABC = tam giác DEC

b) Tính số đo góc CDE ?

#Toán lớp 7

1

L

Luminos

4 tháng 12 2021

Xét tamgiac ABC và tam giác DEC

AC=CD (gt)

BCA=ECD (đđ)

BC=CE (gt)

Vậy tam giác ABC=tam giác DEC _(c-g-c)

⇒ CDE=BAC=90(tương ứng)

Đúng(1)

GD

Gia Đạt Nguyễn

8 tháng 5 2021

Cho tam giác ABC có 3 góc nhọn và 3 đường cao AD,BE,CF a)Chứng minh : tam giác ABE đồng dạng vs tam giác ACF b)Chứng minh :CB×CB=CE×CA

#Toán lớp 8

0

DA

Diệu Anh Hoàng

23 tháng 11 2017 - olm

Cho tam giác ABC. Trên tia đối của tia CA lấy điểm A' sao cho CA'=CA. Trên tia đối của tia CB lấy điểm B' sao cho CB'=CB. Chứng minh tam giác ABC= tam giác A'B'C.

#Toán lớp 7

1

PG

Panda Gấu

24 tháng 11 2017

Xét 2 tam giác ABC và tam giác A'B'C có:

CA = CA'

CB = CB'

Góc ACB = góc A'CB' (2 góc đối đỉnh)

Suy ra: tam giác ABC = tam giác A'B'C

Đúng(0)

HG

Hương Giang

20 tháng 2 2020 - olm

Cho tam giác ABC có CB = 20cm . Kẻ BH vuông góc với AC , biết AH = 9cm , HC = 16cm . Chứng minh tam giác ABC là tam giác vuông.

#Toán lớp 7

1

NH

Nhật Hạ

20 tháng 2 2020

Xét △BHC vuông tại H có: BH² + HC² = BC² (định lý Pytago)

=> BH² + 16² = 20²

=> BH² = 20² - 16² = 400 - 256 = 144

=> BH = 12 (cm)

Xét △BHA vuông tại H có: BH² + AH² = AB² (định lý Pytago)

=> 12² + 9² = AB²

=> AB² = 144 + 81 = 225

=> AB = 15 (cm)

Ta có: AC = AH + HC = 9 + 16 = 25

Xét △ABC có:

AC² = 25² = 625

AB² + BC² = 15² + 20² = 225 + 400 = 625

=> AC² = AB² + AC²

=> △ABC vuông tại A

Đúng(0)

P

PTTD

23 tháng 8 2021

Cho tam giác ABC có góc A = 75 độ, AB = 10,6 cm, \(\widehat{B}\) : \(\widehat{C}\) = 4:3. Tính CA, CB và diện tích tam giác ABC

#Toán lớp 9

2

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 8 2021

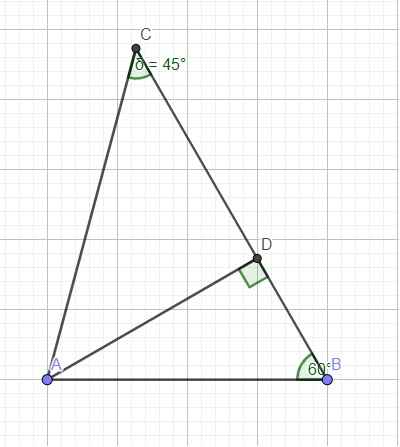
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)

\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)

Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)

Trong tam giác vuông ABD:

\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)

\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)

Trong tam giác vuông ACD:

\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)

\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)

\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)

\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)

Đúng(0)

NV

Nguyễn Việt Lâm

Giáo viên

23 tháng 8 2021

undefined

Đúng(0)

NQ

Nguyễn Quang Linh

28 tháng 2 2022

a/ Cho tam giác ABC vuông tại B có AB=12cm,BC=16cm.Tính AC

b/ Cho tam giác DBC vuông tại C có CB=3cm,BD=5cm.Tính CD

#Toán lớp 7

2

NQ

Nguyễn Quang Linh

28 tháng 2 2022

tôi ko bt, lêu lêu

Đúng(0)

M

Mạnh=_=

28 tháng 2 2022

?

Đúng(0)

DD

Đức Đoàn Minh

24 tháng 1 2018 - olm

cho tam giác abc trên ab lấy m sao cho mb= 1/3 ma. trên cb lấy n sao cho nc= 1/3 cb. diện tích hình tam giác mcn= 21cm vuông. tính diện tích tam giác abc

#Toán lớp 6

0