Cho x,y,z là các số hữu tỉ và 1/x+1/y=1/z. Chứng minh rằng căn(x^2+y^2+z^2) là số hữu tỉ
Giúp mk với ạ!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo giả thiết ta có \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\Leftrightarrow\frac{x+y}{xy}=\frac{1}{z}\Leftrightarrow xz+yz=xy\)
\(\Leftrightarrow xy-xz-yz=0\Leftrightarrow x^2+y^2+z^2+xy-xz-yz=x^2+y^2+z^2\)
\(\Leftrightarrow\left(x+y-z\right)^2=x^2+y^2+z^2\)
\(\Leftrightarrow\sqrt{x^2+y^2+z^2}=\left|x+y-z\right|\)
Mà x, y, z là các số hữu tỉ nên \(\left|x+y-z\right|\)là số hữu tỉ
Vậy \(\sqrt{x^2+y^2+z^2}\)là số hữu tỉ (đpcm)

Ta có:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+0}=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2\left(x+y+z\right)}{xyz}}\)
\(=\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}+\dfrac{2}{xy}+\dfrac{2}{yz}+\dfrac{2}{zx}}=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\) là số hữu tỉ

Thật sự ra mục đích bài này đi chứng minh biểu thức trong ngoặc là scp
Đây là dề thi HSG toán cấp tỉnh Đồng Tháp
Có: \(\sqrt{\left(1+x^2\right)\left(1+y^2\right)\left(1+z^2\right)}\)
\(=\sqrt{\left(x^2+xy+yz+xz\right)\left(y^2+xy+yz+xz\right)\left(z^2+xy+yz+xz\right)}\)
Sau đó thực hiên phân tích đa thức thành nhân tử mỗi ngoặc
\(=\sqrt{\left(x+y\right)^2\left(y+z\right)^2\left(x+z\right)^2}\)
\(=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)là số hữu tỉ
Vậy
Câu số 1b đề thi hsg
Chào anh từ huyện Cao Lãnh
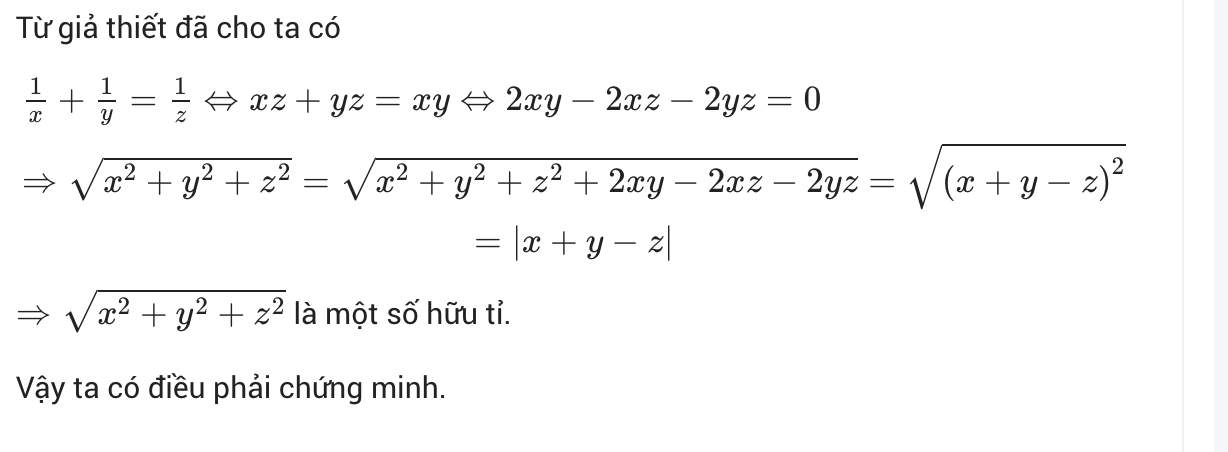
Lời giải:
Từ điều kiện đề bài suy ra $zx+zy=xy$
Khi đó:
$x^2+y^2+z^2=(x+y)^2-2xy+z^2=(x+y)^2+z^2-2(zx+zy)=(x+y)^2+z^2-2z(x+y)=(x+y-z)^2$
$\Rightarrow \sqrt{x^2+y^2+z^2}=|x+y-z|$
Vì $x,y,z$ là các số hữu tỉ nên $\sqrt{x^2+y^2+z^2}=|x+y-z|$ là số hữu tỉ (đpcm)
P/s: Bạn chú ý lần sau gõ đề bằng công thức toán.