Giải phương trình: x3 – 3x2 + 4x + 11 = 0
các bạn giúp mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 4 2022
đây bạn nếu bạn ko hiểu thì lên mạng gõ cách lm bất phương trình mũ 2
nhows
28 tháng 2 2021
4) Ta có: \(\dfrac{2x-5}{5}-\dfrac{x+3}{3}=\dfrac{2-3x}{2}-x-2\)
\(\Leftrightarrow\dfrac{6\left(2x-5\right)}{30}-\dfrac{10\left(x+3\right)}{30}=\dfrac{15\left(2-3x\right)}{30}-\dfrac{30\left(x+2\right)}{30}\)
\(\Leftrightarrow12x-30-10x-30=30-45x-30x-60\)
\(\Leftrightarrow-22x-60=-75x-30\)
\(\Leftrightarrow-22x+75x=-30+60\)
\(\Leftrightarrow53x=30\)
\(\Leftrightarrow x=\dfrac{30}{53}\)
Vậy: \(S=\left\{\dfrac{30}{53}\right\}\)
5) Ta có: \(\dfrac{5x-3}{6}-\dfrac{7x-1}{4}=5\)
\(\Leftrightarrow\dfrac{2\left(5x-3\right)}{12}-\dfrac{3\left(7x-1\right)}{12}=\dfrac{60}{12}\)
\(\Leftrightarrow10x-6-21x+3=60\)
\(\Leftrightarrow-11x-3=60\)
\(\Leftrightarrow-11x=63\)
\(\Leftrightarrow x=-\dfrac{63}{11}\)
Vậy: \(S=\left\{-\dfrac{63}{11}\right\}\)
28 tháng 2 2021
`9,x^3+x^2-2=0`
`x^3-x^2+2x^2-2=0`
`<=>x^2(x-1)+2(x-1)(x+1)=0`
`<=>(x-1)(x^2+2x+2)=0`
`<=>x=1`
`14,x^2-2x+1=0`
`<=>(x-1)^2=0`
`<=>x-1=0`
`<=>x=1`
`15,x^3+3x^2+3x+1=0`
`<=>(x+1)^3=0`
`<=>x+1=0`
`<=>x=-1`
28 tháng 2 2021
Bài 6:
1) Ta có: \(2x\left(x-5\right)-\left(x+3\right)^2=3x-x\left(5-x\right)\)
\(\Leftrightarrow2x^2-10x-\left(x^2+6x+9\right)=3x-5x+x^2\)
\(\Leftrightarrow2x^2-10x-x^2-6x-9-3x+5x-x^2=0\)
\(\Leftrightarrow-14x-9=0\)
\(\Leftrightarrow-14x=9\)
\(\Leftrightarrow x=-\dfrac{9}{14}\)
Vậy: \(S=\left\{-\dfrac{9}{14}\right\}\)
28 tháng 2 2021
`1)2x(x-5)-(x+3)^2=3x-x(5-x)`
`<=>2x^2-10x-x^2-6x-9=3x-5x+x^2`
`<=>x^2-16x-9=x^2-2x`
`<=>14x=-9`
`<=>x=-9/14`
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
a.
\(x^3-7x+6=0\)
\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)
\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
f.
\(x^4-4x^3+12x-9=0\)
\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)
\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)
\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)
CM
10 tháng 10 2019
a) Cách 1: Khai triển HĐT rút gọn được 3 x 2 + 6x + 7 = 0
Vì (3( x 2 + 2x + 1) + 4 < 0 với mọi x nên giải được x ∈ ∅
Cách 2. Chuyển vế đưa về ( x + 3 ) 3 = ( x - 1 ) 3 Û x + 3 = x - 1
Từ đó tìm được x ∈ ∅
b) Đặt x 2 = t với t ≥ 0 ta được t 2 + t - 2 = 0
Giải ra ta được t = 1 (TM) hoặc t = -2 (KTM)
Từ đó tìm được x = ± 1
c) Biến đổi được 
d) Biến đổi về dạng x(x - 2) (x - 4) = 0. Tìm được x ∈ {0; 2; 4}
CM
6 tháng 4 2017
a) x 2 – 4 = 0: đây là phương trình bậc hai; a = 1; b = 0; c = - 4
b) x 3 + 4 x 2 – 2 = 0 : đây không là phương trình bậc hai
c) 2 x 2 + 5 x = 0 : đây là phương trình bậc hai; a = 2; b = 5; c = - 5
d) 4x – 5 = 0 đây không là phương trình bậc hai
e) - 3 x 2 = 0 đây là phương trình bậc hai; a = -3; b = 0; c = 0
PT
1
CM
7 tháng 9 2019
x3 + 3x2 – 2x – 6 = 0
⇔ (x3 + 3x2) – (2x + 6) = 0
⇔ x2(x + 3) – 2(x + 3) = 0
⇔ (x2 – 2)(x + 3) = 0
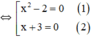
+ Giải (1): x2 – 2 = 0 ⇔ x2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
PT
1
CM
26 tháng 11 2018
x3 + 3x2 + 2x = 0 ⇔ x(x2 + 3x + 2) = 0
⇔ x = 0 hoặc x2 + 3x + 2 = 0 (1)
Giải phương trình (1) ta được các nghiệm x = -1; x = -2
Vậy phương trình đã cho có 3 nghiệm x = 0; x = -1; x = -2
C1 : Cardano (mk chưa học )
C2 : Mode set up -> 5 -> ax^3 + bx^2 + cx + d = 0
PT <=> \(x_1=-1,209...;x_2=2,104....\)
dùng lượng giác hóa cũng được các bạn nhé