Cho \(\Delta ABC\) và \(\widehat{A}< 90^o\) . Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB vẽ tia At sao cho \(\widehat{BAt}=30^o\) và trên tia đó lấy điểm M sao cho AM = AB.Trên nửa...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

LT

Lê Thị Kim Dung

14 tháng 8 2020 - olm

Cho \(\Delta ABC\) và \(\widehat{A}< 90^o\) . Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB vẽ tia At sao cho \(\widehat{BAt}=30^o\) và trên tia đó lấy điểm M sao cho AM = AB.Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia At' sao cho \(\widehat{CAt'}=30^o\) và trên tia đó lấy điểm N sao cho \(AN=AC\) a) Chứng minh \(MC=NB\)b) Tìm số đo góc nhọn tạo bởi hai...

#Hỏi cộng đồng OLM #Toán lớp 7

0

Những câu hỏi liên quan

LT

Lê Thị Kim Dung

15 tháng 8 2020 - olm

Câu hỏi hay

Cho \(\Delta ABC\) và \(\widehat{A}< 90^o\) . Trên nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB vẽ tia At sao cho \(\widehat{BAt}=30^o\) và trên tia đó lấy điểm M sao cho AM = AB.Trên nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC, vẽ tia At' sao cho \(\widehat{CAt'}=30^o\) và trên tia đó lấy điểm N sao cho \(AN=AC\) a) Chứng minh \(MC=NB\)b) Tìm số đo góc nhọn tạo bởi hai...

#Hỏi cộng đồng OLM #Toán lớp 7

0

T

꧁_͏ͥ͏_͏ͣ͏_͏ͫ͏ ¡亗ᵛᶰシ๖ۣۜT๖ۣۜR๖ۣۜÂ๖ۣ...

9 tháng 6 2021

Cho điểm O thuộc đường thẳng xy. Trên cùng một nửa mặt phẳng bờ là đường thẳng xy, vẽ các tia Om, On sao cho \(x\widehat{O}m=25^o\) và \(y\widehat{O}n=75^o\).a) Tính số đo \(m\widehat{O}y\).b) Trên cùng một nửa mặt phẳng bờ chứa Om, không chứa tia Ox, vẽ tia Oz sao cho \(m\widehat{O}z=40^o\). Chứng minh Oz là tia phân giác của \(m\widehat{O}n\).c) Tam giác \(A\widehat{O}B\) có \(A\widehat{O}B=75^o\)và AO=OB=3 cm. Biết...

#Hỏi cộng đồng OLM #Toán lớp 6

3

T

꧁_͏ͥ͏_͏ͣ͏_͏ͫ͏ ¡亗ᵛᶰシ๖ۣۜT๖ۣۜR๖ۣۜÂ๖ۣ...

9 tháng 6 2021

M.n vẽ cả hình hộ mk nha!

R

RedhoodVN

9 tháng 6 2021

Hiện đang suy nghĩ

HN

Hoàng Như Quỳnh

21 tháng 9 2017 - olm

Cho \(\widehat{xOy}\)= 40o. Trên tia Ox lấy 1 điểm A . Vẽ tia At nằm trên cùng nửa mặt phẳng bờ là đường thẳng Ox. Chứa tia Oy sao cho At cắt tia Oy tại B và \(\widehat{OAt}\) = 100o. Gọi tia Am là tia phân giác của \(\widehat{xAt}\) a) Chứng minh Am//Oyb) Trên nửa mặt phẳng không chứa điểm A bờ là đường thẳng Oy. Vẽ tia Bn. Hỏi để Bn//Ox thì số đo hóc OBn phải bằng bao...

#Hỏi cộng đồng OLM #Toán lớp 7

0

KM

Kaori Miyazono

10 tháng 8 2017 - olm

Cho tam giác ABC có \(\widehat{A}< 90^o\) Trên nửa mặt phẳng AB không chứa điểm C vẽ tia Ax vuông góc với B , trên đó lấy điểm D sao cho AD = AB . Trên nửa mặt phẳng bờ AC không chứa điểm B vẽ tia Ay vuông góc với AC , trên đó lấy điểm Esao cho AE = AC a) Chứng minh BE = CD b) Chứng minh \(DE⊥CD\)c) Các đường thẳng AC và ED có thể vuông góc với nhau được không ? Các kết quả trên còn đúng hay...

#Hỏi cộng đồng OLM #Toán lớp 7

2

PL

Phạm Lan Anh

13 tháng 8 2017

đề có sai ko vậy bạn

KM

Kaori Miyazono

13 tháng 8 2017

đề trong sách , ko có sai đâu , ko biết làm thì đừng spam

NT

Nguyễn Tú Hà

11 tháng 7 2023 - olm

Trên đường thẳng AA' lấy điểm O nằm giữa A và A'. Trên một nữa mặt phẳng bờ AA', vẽ tia OB sao cho \(\widehat{AOB}\) = 45* (45 độ). Trên nửa mặt phẳng còn lại vẽ tia OC sao cho \(\widehat{AOC}\) = 90* (90 độ). a) Gọi OB' là tia phân giác của \(\widehat{A'OC}\). Chứng tỏ rằng \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là hai góc đối đỉnh. b) Trên nửa mặt phẳng bờ AA' có chứa tia OB, vẽ tia OD...

#Hỏi cộng đồng OLM #Toán lớp 7

1

LS

Lê Song Phương

11 tháng 7 2023

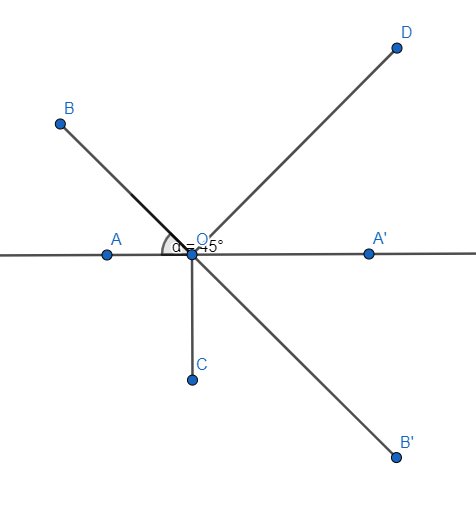
a) Vì OB' là tia phân giác của \(\widehat{A'OC}\) nên \(\widehat{A'OB'}=\dfrac{\widehat{A'OC}}{2}=\dfrac{90^o}{2}=45^o\). Suy ra \(\widehat{AOB}=\widehat{A'OB'}\left(=45^o\right)\). Lại có \(\widehat{AOB}+\widehat{BOA'}=\widehat{AOA'}=180^o\) nên \(\widehat{BOB'}=\widehat{A'OB'}+\widehat{BOA'}=180^o\) hay B, O, B' thẳng hàng. Suy ra \(\widehat{AOB}\) và \(\widehat{A'OB'}\) là 2 góc đối đỉnh.

b) Trên cùng 1 nửa mặt phẳng bờ là đường thẳng AA', ta thấy tia OB nằm giữa 2 tia OA và OD, tia OD lại nằm giữa 2 tia OB và OA', do đó \(\widehat{AOB}+\widehat{BOD}+\widehat{DOA'}=\widehat{AOA'}\) \(\Leftrightarrow45^o+90^o+\widehat{A'OD}=180^o\) \(\Leftrightarrow\widehat{A'OD}=45^o\)

DT

Dinh Thu Giang

6 tháng 7 2019 - olm

cho tam giác ABC,trên 1 nửa mặt phẳng không chứa điểm B có bờ là đường thẳng AC ,vẽ tia Ax vuông góc với AC.Trên tia Ax,lấy điểm M sao cho Am=AC.Trên 1 nửa mặt phẳng không chứa điểm C có bờ là đường thẳng AB,vẽ tia Ay vuông góc với AB.Trên tia By,lấy điểm K sao cho AK=AB.gọi D là trung điểm cua bc.CMR;

a.MK=2AD

b.AD vuông góc với MK

#Hỏi cộng đồng OLM #Toán lớp 7

0

PA

Phúc An Bùi Phan

5 tháng 12 2016

1.cho tam giác ABC có góc A < 90 độ . trên nửa mặt phẳng bờ AB ko chứa điểm C ; vẽ tia Ax vuông góc với AB . trên tia Ax lấy điểm D sao cho AD = AB . trên nửa mặt phẳng bờ AB ko chứa điểm B vẽ tia Ay vuông AC , trên đó lấy điểm E sao cho AE = AC.gọi M là trung điểm BC.chứng minh AM=1/2DE

#Hỏi cộng đồng OLM #Toán lớp 7

1

BT

Bùi Thị Vân

8 tháng 12 2017

Hỏi đáp Toán
Lấy điểm M thuộc tia AM sao cho M là trung điểm của AM.
Ta chứng minh được:
\(\Delta AMB=\Delta M'MC\left(c.g.c\right)\) suy ra AB = BM'.
\(\Delta AMC=\Delta M'MB\left(c.g.c\right)\Rightarrow AC=BM'\), \(\widehat{CAM}=\widehat{BM'M}\).
Theo định lý tổng ba góc trong tam giác:
\(\widehat{M'AB}+\widehat{BM'A}+\widehat{ABM'}=180^o\Leftrightarrow\widehat{BAM'}+\widehat{ABM'}+\widehat{M'AC}=180^o\).
Mà \(\widehat{DAE}+\widehat{BAM}+\widehat{MAC}=180^o\).
Suy ra \(\widehat{DAE}=\widehat{ABM'}\).
Xét tam giác DAE và tam giác ABM' cóL
DA = AB.
BM' = AC = AE.
\(\widehat{DAE}=\widehat{ABM'}\).
Suy ra \(\Delta DAE=\Delta AB'M\left(c.g.c\right)\).
Suy ra DM = AM' = 2AM. (đpcm).

TM

Trần Mai Anh

23 tháng 3 2018 - olm

Cho \(\Delta ABC\)có 3 góc nhọn, M là trung điểm của BC. Trên nửa mặt phẳng chứa điểm C bờ là đường thẳng AB vẽ đoạn thẳng AE vuông góc với AB và AE=AB. Trên nửa mặt phẳng chứa điểm B bờ là đường thẳng AC vẽ đoạn thẳng AD vuông góc với AC và AD=AC.a) Chứng minh BD=CEb) Trên tia đối của tia MA lấy điểm N sao cho MN=MA. Chứng minh \(\widehat{BAC}+\widehat{ACN}=180^o\)c) Gọi I là giao điểm của DE...

#Hỏi cộng đồng OLM #Toán lớp 7

0

LM

Lê Minh Sơn

20 tháng 1 2020 - olm

Cho \(\Delta ABCc\text{ó}\widehat{A}< 90^0.\)Trê nửa mặt phẳng bờ AC không chứa B vẽ tia AX vuông góc với ACvaf lấy trên đó điểm E sao cho AE=AC. Trên nữa mặt phẳng bờ AB không chứa C vẽ tia AY vuông góc với AB và lấy trên đó điểm D sao chi AD=AB.a/Chứng minh DC=BE và \(DC\perp BE\)b/Gọi N là trung điểm của DE. trên tia đối của tia NA lấy điểm Msao cho NA=NM.Chứng minh AB=ME và\(\Delta ABC=\Delta...

#Hỏi cộng đồng OLM #Toán lớp 7

0