1026 - 741 ) : 57 Mik cần gấp , cảm ơn nhiều ạ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
31 tháng 12 2021
Lời giải:
ĐKĐB $\Rightarrow \frac{2}{c}=\frac{a+b}{ab}\Rightarrow c(a+b)=2ab$
Khi đó:
$\frac{a}{b}-\frac{a-c}{c-b}=\frac{a(c-b)-b(a-c)}{b(c-b)}=\frac{ac-ab-ab+bc}{b(c-b)}=\frac{c(a+b)-2ab}{b(c-b)}=\frac{2ab-2ab}{b(c-b)}=0$
$\Rightarrow \frac{a}{b}=\frac{a-c}{c-b}$ (đpcm)
25 tháng 9 2021
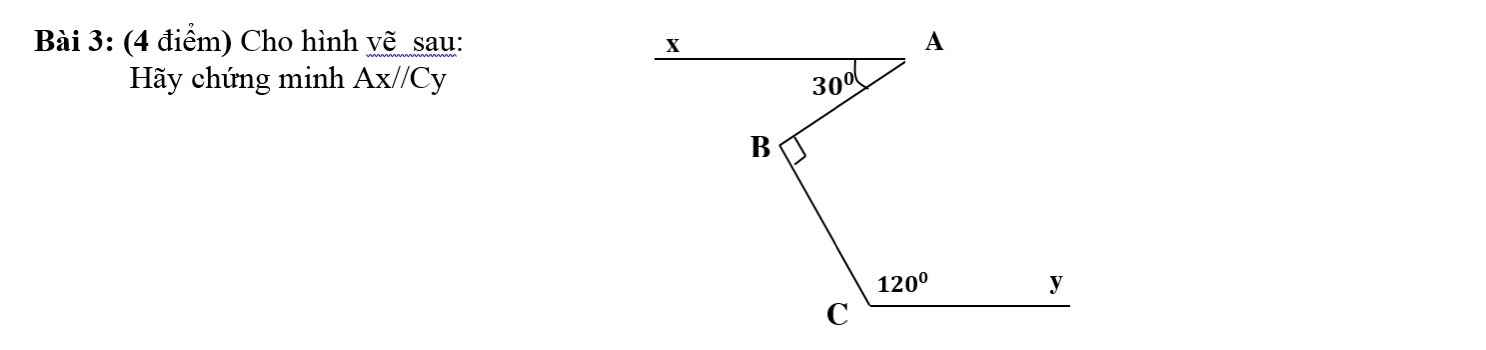
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
27 tháng 3 2022
a) Xét \(\Delta BAD\) và \(\Delta BCE:\)
\(\widehat{B}chung.\)
\(\widehat{D}=\widehat{E}\left(=90^o\right).\)
\(\Rightarrow\Delta BAD\sim\Delta BCE\left(g-g\right).\)
b) Xét \(\Delta ABC:\)
CE là đường cao \(\left(CE\perp AB\right).\)
AD là đường cao \(\left(AD\perp BC\right).\)
Mà F là giao điểm của CE và AD.
\(\Rightarrow BF\) là đường cao.
Xét \(\Delta ABC\) cân tại B:
BF là đường cao (gt).
\(\Rightarrow BF\) là phân giác \(\widehat{ABC}.\)
27 tháng 6 2023
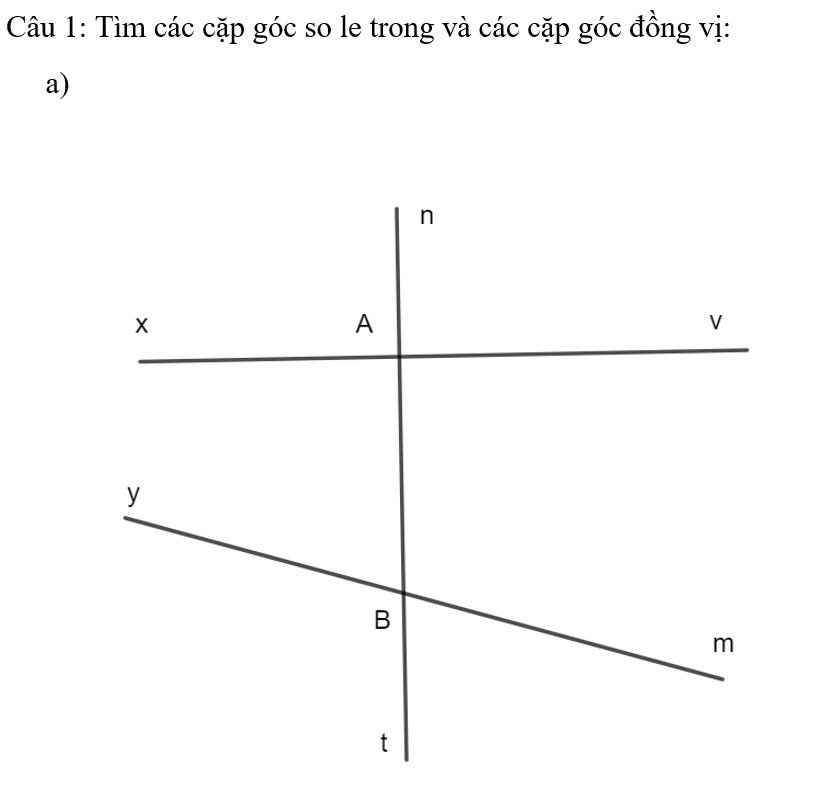
a: So le trong: góc vAB và góc yBA; góc xAB và góc mBA
ĐỒng vị: góc nAx và góc yBA; góc nAv và góc mBA; góc xAB và góc tBy; góc vAB và góc mBt
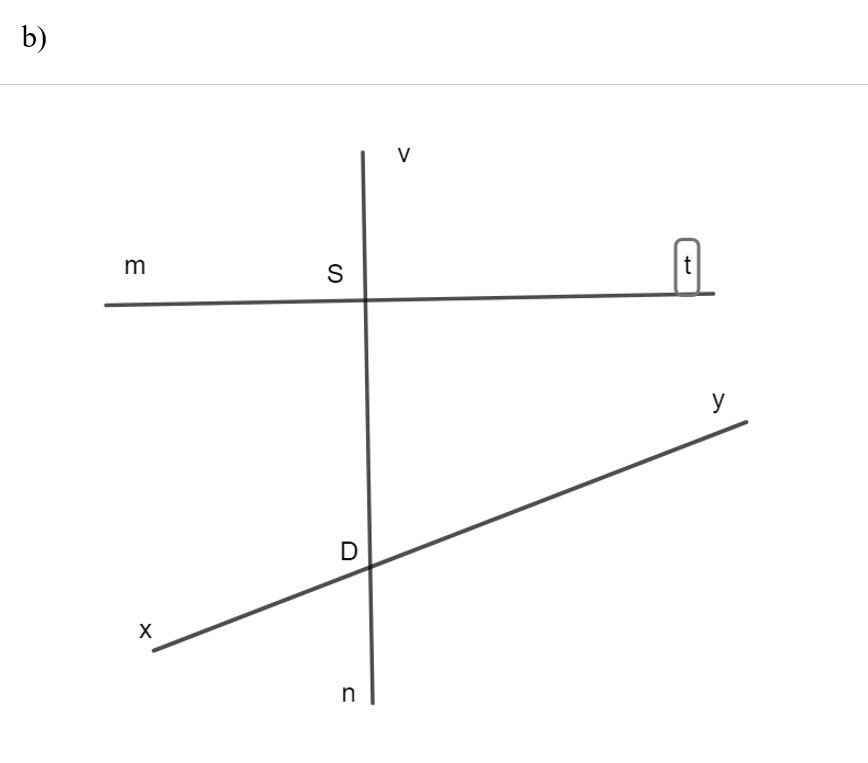
b: So le trong: góc mSD và góc yDS; góc tSD và góc xDS
ĐỒng vị: góc vSm và góc xDv; góc vSt và góc vDy; góc mSn và góc xDn; góc tSD và góc yDn
DR
27 tháng 6 2023
a)Cặp so le trong: xAB và ABm, vAB và ABy
Cặp đồng vị: nAx và ABy, nAv và ABm, xAB và yBt,vAB và mBt
b)Cặp so le trong: mSD và SDy, tSD và SDx
Cặp đồng vị: vSm và SDx, vSt và SDy, nDx và DSm,nDy và DSt
T
1
SA
14 tháng 6 2021
\(A=\dfrac{4x+2\sqrt{x}+2}{2\sqrt{x}+1}=\dfrac{2\sqrt{x}\left(2\sqrt{x}+1\right)+2}{2\sqrt{x}+1}=2\sqrt{x}+\dfrac{2}{2\sqrt{x}+1}\)
\(=2\sqrt{x}+1+\dfrac{2}{2\sqrt{x}+1}-1\ge2\sqrt{\left(2\sqrt{x}+1\right)\cdot\dfrac{2}{2\sqrt{x}+1}}-1=2\sqrt{2}-1\)
=> A \(\ge2\sqrt{2}-1\)
Dấu "=" xảy ra <=> \(2\sqrt{x}+1=\dfrac{2}{2\sqrt{x}+1}\)
<=> \(\left(2\sqrt{x}+1\right)^2=2\) <=> \(\left[{}\begin{matrix}2\sqrt{x}+1=2\\2\sqrt{x}+1=-2\left(loại\right)\end{matrix}\right.\)
<=> \(\sqrt{x}=\dfrac{1}{2}\) <=> \(x=\dfrac{1}{4}\)(tm)
Vậy minA = \(2\sqrt{2}-1\) khi x = 1/4
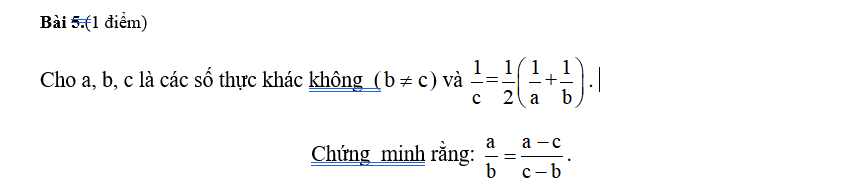
1026 - 741 : 57
= 285 : 57
= 5
Học tốt!!!
( 1026 - 741 ) : 57 = 5
Học tốt nha. ^-^