Cho đồ thị (d): y\(=\left(m-1\right)x-2m+3\)
a, Vẽ (d) khi m \(=\)2
b, Tìm m để (d) là đồ thị hàm số bậc nhất nghịch biến trên R
c,Tìm m để (d) đi qua A(3;5)
d, Tìm m để (d) cách gốc toạn độ một khoảng lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi m = 2 : y = x + 5
TXĐ : D = R.
Tính biến thiên :
bảng biến thiên :
x | -∞ | +∞ | |
y | -∞ |
| +∞ |
Bảng giá trị :
x | 0 | -5 |
y | 5 | 0 |
Đồ thị hàm số y = x + 5 là đường thẳng đi qua hai điểm A(0, 5) và B(-5; 0).
b/(dm) đi qua điểm A(4, -1) :
4 = (m -1)(-1) +2m +1
<=> m = 2
3. hàm số nghịch biến khi : a = m – 1 < 0 <=> m < 1
4.(dm) đi qua điểm cố định M(x0, y0) :
Ta được : y0 = (m -1)( x0) +2m +1 luôn đúng mọi m.
<=> (x0 + 2) m = y0 – 1 + x0(*)
(*) luôn đúng mọi m khi :
x0 + 2= 0 và y0 – 1 + x0 = 0
<=> x0 =- 2 và y0 = 3
Vậy : điểm cố định M(-2, 3)

a: Để hàm số là hàm số bậc nhất thì 2m-3<>0
hay m<>3/2
b: Để hàm số đồng biến thì 2m-3>0
hay m>3/2
Để hàm số nghịch biến thì 2m-3<0
hay m<3/2

Thay A(0,1) vào hàm số y ta có:
\(\left(m-3\right).4+3m-1=1\Leftrightarrow4m-12+3m-1=0\)
\(\Leftrightarrow7m-13=0\Leftrightarrow7m=13\Leftrightarrow m=\dfrac{13}{7}\)

Bài 1:
a: Để (d) là hàm số bậc nhất thì 2m-2<>0
hay m<>1
b: Để (d) là hàm số đồng biến thì 2m-2>0
hay m>1
c: Hàm số (d') đồng biến vì a=4>0
Bài 2:
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-x+6=3x-6\\y=-x+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)

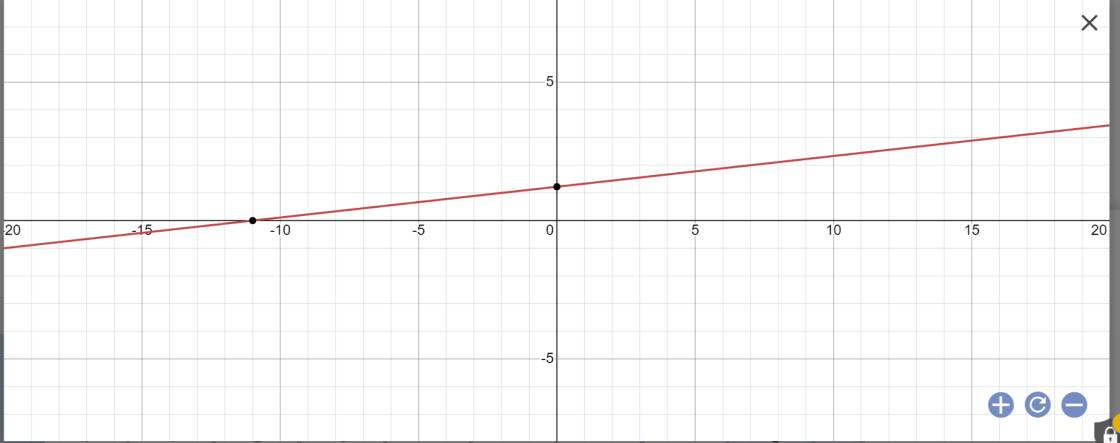
Thay x=-11 và y=0 vào (d), ta được:
-11(m-3)+2m-5=0
=>-11m+33+2m-5=0
=>-9m+28=0
=>m=28/9
=>(d): y=1/9x+56/9-5=1/9x+11/9

a) Khi m =2 thì y = 3x - 1
(Bạn tự vẽ tiếp)
b) Để \((d)//(d_{1})\) thì \(\begin{cases} 2m-1=-3\\ -3m+5\neq2 \end{cases} \) ⇔ \(\begin{cases} m=-1\\ m\neq1 \end{cases} \) ⇔ \(m=-1\)
c)
Để \((d) ⋂ (d1)\) thì \(2m-1\neq-3 \) ⇔ \(m\neq-1\)
Giao điểm của 2 đường thẳng thuộc trục tung => x=0
Khi đó, ta có: \(y=-3.0+2=2\)
⇒ Điểm \((0;2)\) cũng thuộc đường thẳng (d)
⇒ \(2=(2m-1).0-3m+5\) ⇔ \(m=1\) (TM)
a, Bạn tự vẽ nhaaaa
b,c, Bạn kia làm r nên mình làm ý d thôi nha
d,Giả sử M(x';y') là điểm cố định mà đồ thị hàm số đi qua với mọi m
\(\Leftrightarrow\) y' = (m-1)x' -2m+3
\(\Leftrightarrow\) y' + x' -3 = mx' - 2m
\(\Leftrightarrow\) y' +x' -3 = m(x' -2)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x'-2=0\\y'+x'-3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x'=2\\y'=1\end{matrix}\right.\)
\(\Rightarrow\) Điểm M(2;1) cố định mà đồ thị hàm số đi qua với mọi m
Vì điểm M(2;1) nên OM= \(\sqrt{1^2+2^2}=\sqrt{5}\left(\text{đ}v\right)\)
Kẻ OH\(\perp\left(d\right)\Rightarrow OH\le OM\Leftrightarrow OH\le\sqrt{5}\)
Dấu "=" \(\Leftrightarrow\) H trùng M \(\Leftrightarrow OM\perp\left(d\right)\)
Do OM là một đường thẳng đi qua gốc toạ độ nên OM: y=ax(a khác 0)
nên 1= 2a nên OM: y =\(\frac{1}{2}x\)
Mà OM vuông (d) nên a.a'=-1 nên (m-1)\(\frac{1}{2}=-1\) \(\Leftrightarrow m=-1\)
Kl: m=-1 để (d) cách gốc toạ độ một khoảng lớn nhất là \(\sqrt{5}\left(\text{đ}v\right)\)
c ) THay tọa độ A ta có
\(5=\left(m-1\right)3-2m+3\Leftrightarrow m-5=0\Leftrightarrow m=5\)