Cho hàm số \(y=\frac{mx-m^2-2}{-x+1}\) (m là tham số thực) thỏa mãn \(max_{\left[-4;-2\right]}y=\frac{-1}{3}\). Mệnh đề nào sau dưới đây đúng?
A ,\(\frac{-1}{2}< m< 0\) B, \(m>4\) C, \(1\le m< 3\) D, \(-3< m< \frac{-1}{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm bậc nhất trên bậc nhất luôn đơn điệu trên mỗi khoảng xác định
\(\Rightarrow\) GTLN của hàm trên \(\left[2;5\right]\) rơi vào 1 trong 2 đầu mút
Hay \(\max\limits_{\left[2;5\right]}y=max\left\{y\left(2\right);y\left(5\right)\right\}\)
\(y\left(2\right)=\frac{m+3}{-1}=-m-3\)
\(y\left(5\right)=\frac{m+6}{-4}\)
TH1: nếu \(y_{max}=y\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}-m-3>\frac{m+6}{-4}\\-m-3=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< -2\\m=-7\end{matrix}\right.\)
\(\Rightarrow m=-7\)
TH2: nếu \(y_{max}=y\left(5\right)\Leftrightarrow\left\{{}\begin{matrix}\frac{m+6}{-4}>-m-3\\\frac{m+6}{-4}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>-2\\m=-22\left(l\right)\end{matrix}\right.\)
Vậy \(m=-7\)

Xét hàm \(f\left(x\right)=\dfrac{x+m}{x+1}\) có \(f'\left(x\right)=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+m\right)\left(x+1\right)'}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x-1\right)^2}\)
Cho \(f'\left(x\right)=\dfrac{1-m}{\left(x-1\right)^2}=0\Leftrightarrow m=1\)
Khi đó \(f\left(x\right)=\dfrac{x+1}{x+1}=1\)
\(\Rightarrow max_{\left[0;1\right]}\left|f\left(x\right)\right|+min_{\left[0;1\right]}\left|f\left(x\right)\right|=1+1=2\) ( thỏa mãn )
Vậy \(m=1\) thỏa mãn bài toán.
Xét \(m\ne1\), ta thấy \(f\left(x\right)\) đơn điệu trên \(\left[0;1\right]\), xét các trường hợp:
*) \(f\left(0\right).f\left(1\right)\le0\Leftrightarrow\dfrac{m+1}{2}\cdot m\le0\) \(\Leftrightarrow-1\le m\le0\)
\(\Rightarrow\left\{{}\begin{matrix}min_{\left[0;1\right]}\left|f\left(x\right)\right|=0\\max_{\left[0;1\right]}\left|f\left(x\right)\right|=max\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\end{matrix}\right.\)
Khi đó: \(max_{\left[0;1\right]}\left|f\left(x\right)\right|+min_{\left[0;1\right]}\left|f\left(x\right)\right|=2\)
\(\Leftrightarrow0+\dfrac{\left|\dfrac{m+1}{2}+m\right|+\left|\dfrac{m+1}{2}-m\right|}{2}=2\)
\(\Leftrightarrow\left|\dfrac{3m+1}{2}\right|+\left|\dfrac{-m+1}{2}\right|=4\)
\(\Leftrightarrow\left|3m+1\right|+\left|m-1\right|=8\) (1)
Xét các trường hợp:
+) \(m\le\dfrac{-1}{3}\) : \(\left(1\right)\Leftrightarrow-3m-1-m+1=8\Leftrightarrow m=-2\) ( loại )
+) \(m\ge1\) : \(\left(1\right)\Leftrightarrow3m+1+m-1=8\Leftrightarrow m=2\) ( loại )
+) \(-\dfrac{1}{3}< m< 1\) : \(\left(1\right)\Leftrightarrow3m+1-m+1=8\Leftrightarrow m=3\) ( loại )
*) \(f\left(0\right)\cdot f\left(1\right)>0\Leftrightarrow\dfrac{m+1}{2}\cdot m>0\Leftrightarrow\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}min_{\left[0;1\right]}\left|f\left(x\right)\right|=min\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\\max_{\left[0;1\right]}\left|f\left(x\right)\right|=max\left\{\dfrac{\left|m+1\right|}{2};\left|m\right|\right\}\end{matrix}\right.\)
Khi đó: \(min_{\left[0;1\right]}\left|f\left(x\right)\right|+max_{\left[0;1\right]}\left|f\left(x\right)\right|=2\)
\(\Leftrightarrow\dfrac{\left|\left|\dfrac{m+1}{2}+m\right|-\left|\dfrac{m+1}{2}-m\right|\right|}{2}+\dfrac{\left|\left|\dfrac{m+1}{2}+m\right|\right|+\left|\left|\dfrac{m+1}{2}-m\right|\right|}{2}=2\)
\(\Leftrightarrow\dfrac{\left|\left|3m+1\right|-\left|m-1\right|\right|}{4}+\dfrac{\left|\left|3m+1\right|+\left|m-1\right|\right|}{4}=2\)
\(\Leftrightarrow\dfrac{2\left|3m+1\right|}{4}=2\)
\(\Leftrightarrow\left|3m+1\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{-5}{3}\end{matrix}\right.\)
Tóm lại ở cả 2 trường hợp thì ta có \(m\in\left\{1;\dfrac{-5}{3}\right\}\) thỏa mãn đề bài.
Vậy \(S=\left\{1;\dfrac{-5}{3}\right\}\) có \(2\) phần tử.

- Phương trình hoành độ giao điểm của (P) và (d'):
\(-x^2=mx-4\Leftrightarrow x^2+mx-4=0\left(1\right)\)
\(a=1;b=m;c=-4\)
\(\Delta=b^2-4ac=m^2-4.\left(1\right).\left(-4\right)=m^2+16>0\)
Vì \(\Delta>0\) nên (P) và (d) luôn cắt nhau tại hai điểm phân biệt có hoành độ x1, x2.
Theo định lí Viete cho phương trình (1) ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{m}{1}=-m\\x_1x_2=\dfrac{c}{a}=\dfrac{-4}{1}=-4\end{matrix}\right.\)
Ta có: \(\left(x_1-x_2\right)^2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)=18\)
\(\Rightarrow\left(-m\right)^2-2.\left(-4\right)-\left(-m\right)-18=0\)
\(\Leftrightarrow m^2+m-12=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-3\end{matrix}\right.\)
Vậy m=4 hay m=-3.

Ta có : \(y'=-x^2+2mx+m-2\Rightarrow\Delta'=m^2+m-2\)
Hàm số đồng biến trên đoạn có độ dài bằng 4 <=> phương trình y' =0 có 2 nghiệm phân biệt \(x_1;x_2\) và thỏa mãn :
\(\left|x_1-x_2\right|=4\Leftrightarrow\begin{cases}\Delta'>0\\\left|x_1-x_2\right|=4\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\\left(x_1+x_2\right)^2-4x_1.x_2=16\end{cases}\)
\(\Leftrightarrow\begin{cases}m^2+m-2>0\\4m^2+4\left(m-2\right)=16\end{cases}\)
\(\Leftrightarrow m=2\) hoặc \(m=-3\)
Kết luận \(m=2\) hoặc \(m=-3\) thì hàm số đồng biến trên đoạn có độ dài bằng 4

Đáp án C
Ta có: y ' = − 1 − m x − 1 2
· Trường hợp 1: nếu y ' > 0 ⇒ m < − 1 , lúc này hàm số đồng biến
⇒ min 2 ; 4 y = y 2 = 2 + m 2 − 1 = 3 ⇒ m = 1 (mâu thuẫn với m < -1) => loại
· Trường hợp 2: nếu y ' < 0 ⇒ m > − 1 , lúc này hàm số nghịch biến
⇒ min 2 ; 4 y = y 4 = 4 + m 4 − 1 = 3 ⇒ m = 5 (thỏa mãn với m > -1) => chọn
Đối chiếu 4 đáp án thì có đáp án C là thỏa mãn.

Đáp án C
Phương pháp: Hàm số bậc nhất trên bậc nhất y = a x + b c x + d a d - b c ≠ 0 luôn đơn điệu trên từng khoảng xác định của nó.
TH1: Hàm số đồng biến trên [2;4] => m a x 2 ; 4 y = y ( 4 )
TH2: Hàm số nghịch biến trên [2;4] => m a x 2 ; 4 y = y ( 2 )
Cách giải: Tập xác định: D = R\{1}
Ta có: 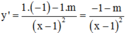
TH1: ![]()
![]() =>Hàm số đồng biến trên
=>Hàm số đồng biến trên 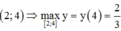
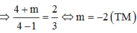
TH2: ![]()
![]() => Hàm số nghịch biến trên
=> Hàm số nghịch biến trên ![]()
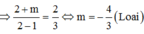
Vậy m = –2
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn
\(y'=\frac{m^2+m+2}{\left(1-x\right)^2}=\frac{\left(m+\frac{1}{2}\right)^2+\frac{7}{4}}{\left(1-x\right)^2}>0\)
Hàm đồng biến trên \(\left[-4;-2\right]\)
\(\Rightarrow\max\limits_{\left[-4;-2\right]}y=y\left(-2\right)=-\frac{m^2+2m+2}{3}\)
\(\Rightarrow-\frac{m^2+2m+2}{3}=-\frac{1}{3}\Rightarrow m^2+2m+2=1\)
\(\Rightarrow m=-1\)