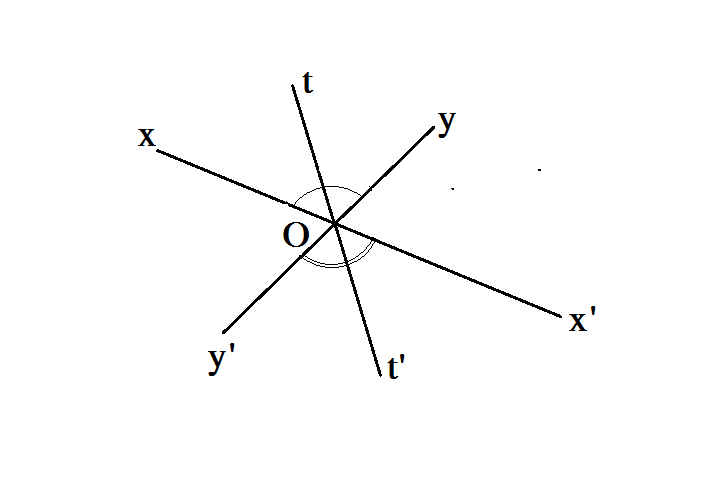
Cho hình vẽ sau:
Biết hai đoạn thẳng xx' và yy' cắt nhau tại O tạo thành một góc (khác góc vuông)
Ot và Ot' lần lượt là tia phân giác của hai góc xOy và góc x'Oy'.
Chứng minh góc tOt' bằng 180o.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) ta có O1+O2=180=> O2=180-O1=180-36=144
TA CÓ : O1=O3 =36 ( đối đỉnh )
O2=O4 =144 ( đối đỉnh)
b) ta có góc tOt'= góc tOx+O4+góc y'Ot'= \(\frac{36}{2}\)+144+ \(\frac{36}{2}\)=180
=> Ot và Ot' nằm trên cùng đường thẳng
mặt khác Ot và Ot' cùng chung gốc O
=> Ot và Ot' là 2 tia đối

ta có: xx' cắt yy' tại O
=> góc xOy = góc x'Oy' ( đối đỉnh)
=> góc xOy/2 = góc x'Oy'/2
mà góc O1 = góc xOy/2 ( định lí tia phân giác)
góc O2 = góc xOy/2 ( định lí tia phân giác)
=> góc O1 = góc O2
mà góc O1 = góc xOy/2 => góc O1. 2 = góc xOy
mà góc xOy + góc xOy' = 180 độ
=> góc O1 .2 + góc xOy' = 180 độ
góc O1 + góc O1 + góc xOy' = 180 độ
=> góc O1 + góc O2 + góc xOy' = 180 độ ( góc O1 = góc O2)
=> Ot' là tia đối của tia Ot ( định lí)