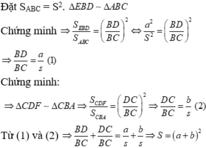Cho tam giác ABC ,qua điểm E trên cạnh AC kẻ đường thẳng song song với BC ,và kẻ EF song song với AB(D thuộc AB,F thuộc BC).Đặt diện tích tam giác ADE là S1,diện tích tam giác CEF là S2 ,diện tích tứ giác BDEF là S. S^2=4*S1*S2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 9 2015
+) ED // BF; FE // BD => Tứ giác FBDE là hbh => DE = BF
+) Dễ có: tam giác ADE đồng dạng với ABC => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2\) (*) ( tỉ số diện tích = bình phương tỉ số đồng dạng)
Tam giác CFE đồng dạng với tam giác CAB => \(\frac{S_{CFE}}{S_{ABC}}=\left(\frac{CF}{BC}\right)^2\)
=> \(\frac{S_{ADE}}{S_{ABC}}:\frac{S_{CFE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2:\left(\frac{CF}{CB}\right)^2\) => \(\frac{S_{ADE}}{S_{CFE}}=\left(\frac{DE}{FC}\right)^2=\frac{101}{143}\) => \(\left(\frac{BF}{CF}\right)^2=\frac{101}{143}\)
=> \(\frac{BF}{CF}=\sqrt{\frac{101}{143}}\) => \(\frac{BF}{CF+BF}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}\)=> \(\frac{BF}{BC}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}=\frac{DE}{BC}\)
Thay vào (*) => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{\sqrt{101}}{\sqrt{101}+\sqrt{143}}\right)^2=\frac{101}{S_{ABC}}\) => S(ABC) =....
CM
11 tháng 12 2019
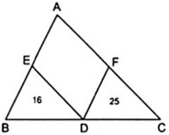
Đặt S A B C = S . Vì DE//AC nên Δ BED ∼ Δ BAC
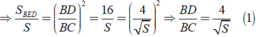
Lại có DF//AB nên Δ CDF ∼ Δ CBA
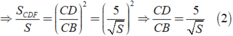
Cộng theo vế của đẳng thức ( 1 ) và ( 2 ) ta được:
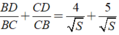
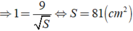
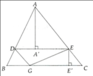
Vậy diện tích của tam giác ABC là 81 c m 2
CH
Cô Hoàng Huyền
Admin
VIP
14 tháng 11 2016
Giả sử BM = x; MC = 1. Khi đó ta có \(\Delta BEM\sim\Delta MDC\) theo tỉ lệ x. Vậy \(x^2=\frac{S_1}{S_2}=\frac{103}{145}\Rightarrow x=\sqrt{\frac{103}{145}}\)
Lại có \(\Delta BEM\sim\Delta BAC\) theo tỉ lệ \(\frac{x}{x+1}\) nên \(\frac{S_1}{S_{ABC}}=\left(\frac{x}{x+1}\right)^2\Rightarrow S_{ABC}=\frac{103}{\left(\frac{x}{x+1}\right)^2}\approx492,42\left(cm^2\right).\)