Question

[lili hương]

1 cho hình chóp S.ABCD đều có SA=AB=a. Góc giữa SA và CD là

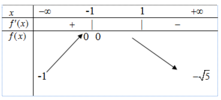
2 Gọi M,m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y=\(\frac{\sqrt{x^2-1}}{x-2}\) trên tập hợp D= \(\left(-\infty;-1\right)\cup\left[1;\frac{3}{2}\right]\) . Tính M+m

A .P=2

B P=0

C P=-\(\sqrt{5}\)

D P = \(\sqrt{3}\)

3 Tập nghiệm của bất phương trình \(\left(\frac{1}{1+a^2}\right)^{2x+1}\) >1 ( với a là tham số , a#0) là

4 Trong ko gian cho tam giác ABC vuông tại A ,AB=a, AC=\(a\sqrt{3}\) . Tính độ dài đường sinh l của hình nón có được khi quay tam giác ABC xung quanh trục AB

5 Viết công thức tính V của vật thể nằm giữa hai mp x=0, x=ln4, biết khi cắt vật thể bởi mặt phẳng vuông góc với trục hoành tại điểm có hoành độ x (\(0\le x\le ln4\)), ta được thiết diện là một hình vuông cạnh là \(\sqrt{xe^x}\)

6 cho cấp số cộng có u1=0 và công sai d =3. Tổng của 26 số hạng đầu tiên của cấp số cộng đó bằng bao nhiêu

7 cho khối chóp tam giác có đường cao bằng 100cm và cạnh đáy 20cm,21cm,29cm. Tính thể tích khối chóp

8 cho hai điểm A(-2;1;2),B(0;-1;1).Phương trình mặt cầu đường kính AB

9 Cho hình lập phương ABCD.\(A^,B^,C^,D^,\) , gÓC giữa hai đường thẳng \(B^,A\) và CD bằng

10 Tổng giá trị lớn nhất và nhỏ nhất của hàm số y= \(\sqrt{2-x^2}-x\) bằng

A \(2+\sqrt{2}\)

B 2

C 1

D \(2-\sqrt{2}\)

11 Số giao điểm của đồ thị hàm số y= \(x^2/x^2-4/\) với đường thẳng y=3 là

12 Tập nghiệm của bất pt \(log_{\frac{1}{3}}\left(x+1\right)>log_3\left(2-x\right)\) là S =(a;b) \(\cup\) (c;d) với a,b,c,d là các số thực. Khi đó a+b+c+d bằng

A 4

B 1

C 3

D 2

13 Tính thể tích khối tròn xoay sinh ra khi quay tam giác đều ABC cạnh bằng 1 quanh AB

14 trong ko gian với hệ trục tọa độ Oxyz, cho đường thẳng d :\(\frac{x-1}{1}=\frac{y+2}{-1}=\frac{z}{2}\) . MẶT phẳng (P) đi qua điểm M (2;0;-1) và vuông góc vói d có pt là

A x-y+2z=0

B x-2y-2=0

C x+y+2z=0

D x-y-2z=0

Answer 1

[Akai Haruma]

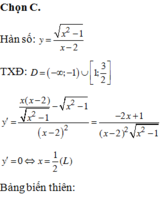
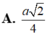
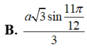
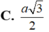
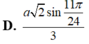
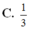
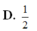
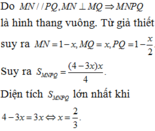
Bài 14:

Vecto chỉ phương của đường thẳng $d$ là: $\overrightarrow{u_d}=(1; -1; 2)$

Mp $(P)$ vuông góc với $d$ nên nhận $\overrightarrow{u_d}$ là vecto pháp tuyến

Do đó PTMP $(P)$ là:

$1(x-x_M)-1(y-y_M)+2(z-z_M)=0$

$\Leftrightarrow x-y+2z=0$

Đáp án A

Answer 2

[Akai Haruma]

Bài 13:

Khi quay tam giác đều ABC quanh cạnh AB thì ta thu được một khối hình là hợp của 2 hình nón (ngược chiều nhau) có cùng bán kính đáy $r$ là đường cao của tam giác đều, tức là $r=\frac{\sqrt{3}}{2}.1=\frac{\sqrt{3}}{2}$ và đường cao là $h=\frac{AB}{2}=\frac{1}{2}$

Thể tích 1 hình nón: $V_n=\frac{1}{3}\pi r^2h=\frac{\pi}{8}$

Do đó thể tích của khối hình khi quay tam giác đều ABC quanh AB là: $2V_n=\frac{\pi}{4}$