Cho một lăng kính bên phải ABC.A'B'C' mà AB = 9 cm; BC = 15 cm; AC = 12 cm.
Có .... đường thẳng vuông góc với đường thẳng AB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .



Khi tia tím có góc lệch cực tiểu thì rt1 = rt2 = A/2 = 30o
Suy ra sini = n.sint1 = √3/2⟹ i = 30o.
Chọn đáp án C

a) Góc lệch có giá trị cực tiểu khi: 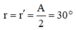
Áp dụng định luật khúc xạ ánh sáng ta có:

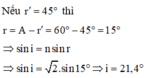
Để tia sáng không ló ra được ở mặt bên thứ 2 thì phải quay lăng kính quanh cạnh lăng kính một góc nhỏ nhất là
![]()

Đáp án cần chọn là: A
Vì tia tím truyền đối xứng qua lăng kính nên ta có: góc lệch D cực tiểu
i 1 t = i 2 t = i r 1 t = r 2 t = A 2 = 30 °
D m = 2 i - A → i = D m + 60 2
Mặt khác, ta có:
sin i = n t sinr 1 t ↔ sin D m + 60 2 = 3 sin 30 0
→ sin D m + 60 2 = 3 2 → D m + 60 2 = 60 → D m = 60 0 , i = 60 0
+ Tia ló đỏ truyền đối xứng qua lăng kính thì:
i 1 d = i 2 d = i ' r 1 d = r 2 d = A 2 = 30 °
→ D m = 2 i ' - A → i ' = D m + 60 2
Mặt khác, ta có:
sin i = n d sinr 1 d ↔ sin D m + 60 2 = 2 sin 30 0
→ sin D m + 60 2 = 2 2 → D m + 60 2 = 45 → D m = 30 0 , i = 45 0
Vậy ta cần phải quay góc: α = i − i ' = 60 − 45 = 15 0

Đáp án cần chọn là: B
Áp dụng định luật khúc xạ ánh sáng tại điểm tới I của mặt thứ nhất, ta có:
sin i 1 = n sinr 1 ↔ sin 45 = 2 sinr 1 → sinr 1 = 1 2 → r 1 = 30 0
Vì tia ló ra khỏi mặt thứ 2 đi vuông góc nên: i 2 = 0 → r 2 = 0
Ta có: A = r 1 + r 2 = 30 + 0 = 30 0