Câu 1: Một con lắc lò xo khi dao động tự do thì ở thời điểm t1 vật có li độ x1 = 1 cm, và có vận tốc v1= 20 π cm/s. Đến thời điểm t2 vật có li độ x2 = 2 cm và có vận tốc v2 = 10 π cm/s. Lấy π2 = 10. Trong cùng một điều kiện về lực cản của môi trường thì biểu thức ngoại lực điều hoà nào sau đây làm cho con lắc dao động cưỡng bức với biên độ nhỏ nhất trong giai đoạn ổn định?
A. F = F0cos(2πt + π). B. F = F0cos(20πt + 0,5π).
C. F = F0cos(10πt + 0,25π). D. F = F0cos8πt.


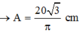
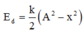
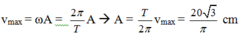
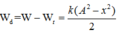
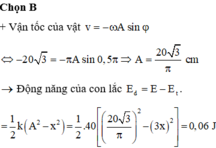


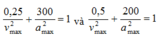


\(x_1^2+\frac{v_1^2}{\omega^2}=x_2^2+\frac{v_2^2}{\omega^2}\Rightarrow\omega=\sqrt{\frac{v_2^2-v_1^2}{x_1^2-x_2^2}}=10\pi\)
Do pt của 4 ngoại lực có biên độ bằng nhau, để con lắc dao động với biên độ nhỏ nhất trong giai đoạn ổn định thì \(\left|\omega-\omega_F\right|\) là lớn nhất
\(\Rightarrow\) Đáp án B đúng (không chắc lắm :( )