Cho 5 hình tròn chồng lên nhau như hình trên. Chứng minh những hình trăng khuyết tạo thành đều có diện tích bằng nhau.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
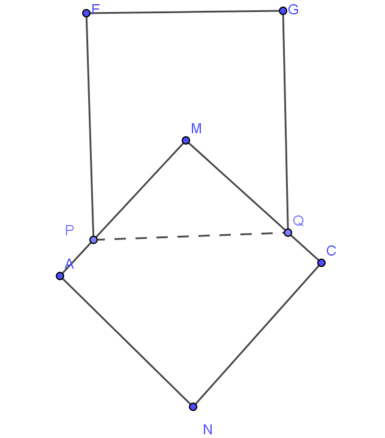
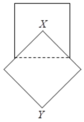
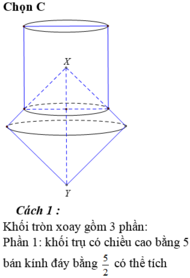
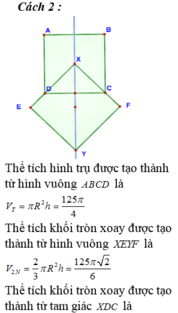
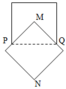
Gọi V 1 là thể tích khối trong xoay khi xoay hình vuông EGQP quanh MN. Khối này có bán kính đáy R = 1 2 E G = 5 2 và đường cao = EP = 5 => V 1 = 5 . 5 2 2 π = 125 4 π
Gọi V 2 là thể tích khối tròn xoay khi xoay hình vuông AMCN quanh MN, khối này là hợp lại của 2 khối nón đêu có bán kính đáy R = 1 2 A C = 5 2 2 Đường cao h = 1 2 M N = 5 2 2 => V 2 = 2 . 1 3 . 5 2 2 . 5 2 2 2 π = 125 2 6 π
Gọi V 3 là thể tích của khối nón tròn xoay khi quay MPQ quanh MN, khối này óc bán kính đáy R = 1 2 P Q = 5 2 đường cao h = d ( M ; P Q ) = 5 2 => V 3 = 1 3 . 5 2 . 5 2 2 . π = 125 12 π
Ta có thể tích của toàn khối tròn xoay V = V 1 + V 2 - V 3 = 125 1 + 2 π 6

Muốn tính diện tích hình hoa, lấy diện tích hình vuông trừ phần còn lại. Diện tích phần còn lại=(S hình vuông- S hình tron)x2=(4x4-2x2x3,14)x2(*) S hình hoa = 4x4-(*) =4*4-2*(4*4-4*3,14)

Hình A gồm 4 ô vuông.
Hình B gồm 3 ô vuông.
Hình C gồm 4 ô vuông.
Hình D gồm 5 ô vuông.
Hình E gồm 4 ô vuông.
a) Các hình có diện tích bằng nhau là: hình A, hình C và hình E
b) Hình D có diện tích lớn hơn diện tích hình A.
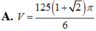
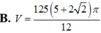
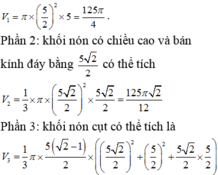
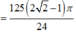
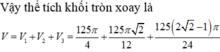
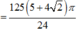
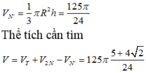

có năm hình tròn