Tìm m để phương trình sin2x = 7m + 3 có nghiệm \(x\in\left[0;\frac{7\pi}{12}\right]\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đức Trí
VIP
9 tháng 9 2023
\(4sin\left(x+\dfrac{\pi}{3}\right).cos\left(x-\dfrac{\pi}{6}\right)=m^2+\sqrt[]{3}sin2x-cos2x\)
\(\Leftrightarrow4.\left(-\dfrac{1}{2}\right)\left[sin\left(x+\dfrac{\pi}{3}+x-\dfrac{\pi}{6}\right)+sin\left(x+\dfrac{\pi}{3}-x+\dfrac{\pi}{6}\right)\right]=m^2+2.\left[\dfrac{\sqrt[]{3}}{2}.sin2x-\dfrac{1}{2}.cos2x\right]\)
\(\Leftrightarrow2\left[sin\left(2x+\dfrac{\pi}{6}\right)+sin\left(2x-\dfrac{\pi}{6}\right)\right]=m^2+2\)
\(\Leftrightarrow2.2sin2x.cos\dfrac{\pi}{6}=m^2+2\)
\(\Leftrightarrow2.2sin2x.\dfrac{\sqrt[]{3}}{2}=m^2+2\)
\(\Leftrightarrow2\sqrt[]{3}sin2x.=m^2+2\)
\(\Leftrightarrow sin2x.=\dfrac{m^2+2}{2\sqrt[]{3}}\)
Phương trình có nghiệm khi và chỉ khi
\(\left|\dfrac{m^2+2}{2\sqrt[]{3}}\right|\le1\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{m^2+2}{2\sqrt[]{3}}\ge-1\\\dfrac{m^2+2}{2\sqrt[]{3}}\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2\ge-2\left(1+\sqrt[]{3}\right)\left(luôn.đúng\right)\\m^2\le2\left(1-\sqrt[]{3}\right)\end{matrix}\right.\)
\(\Leftrightarrow-\sqrt[]{2\left(1-\sqrt[]{3}\right)}\le m\le\sqrt[]{2\left(1-\sqrt[]{3}\right)}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 1
Phương trình trên có nghiệm kép khi:
\(\Delta'=\left(m-9\right)^2-\left(m+7\right)\left(-7m+15\right)=0\)
\(\Leftrightarrow8\left(m^2+2m-3\right)=0\)
\(\Leftrightarrow8\left(m-1\right)\left(m+3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}m=1\\m=-3\end{matrix}\right.\)
- Với \(m=1\) nghiệm kép của pt là \(x=\dfrac{m-9}{m+7}=-1\)
- Với \(m=-3\) nghiệm kép của pt là \(x=\dfrac{m-9}{m+7}=-3\)
TB
1
16 tháng 10 2021
C) Pt \(\Rightarrow m\cdot\dfrac{1-cos2x}{2}-\left(m-1\right)sin2x+\left(2m+1\right)\cdot\dfrac{1+cos2x}{2}=0\)
\(\Rightarrow\left(m+1\right)cos2x-\left(2m-2\right)sin2x=-1-3m\)
Pt có nghiệm: \(\Leftrightarrow\) \(\left(m+1\right)^2+\left[-\left(2m-2\right)\right]^2\ge\left(1+3m\right)^2\)
\(\Rightarrow\dfrac{-3-\sqrt{13}}{2}\le m\le\dfrac{-3+\sqrt{13}}{2}\)
Pt vô nghiệm: \(\Rightarrow\left\{{}\begin{matrix}m>\dfrac{-3+\sqrt{13}}{2}\\m< \dfrac{-3-\sqrt{13}}{2}\end{matrix}\right.\)
30 tháng 7 2021
b) Thay x=2 vào pt, ta được:
\(4\left(m^2-1\right)-4m+m^2+m+4=0\)
\(\Leftrightarrow4m^2-4-4m+m^2+m+4=0\)
\(\Leftrightarrow5m^2-3m=0\)
\(\Leftrightarrow m\left(5m-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=\dfrac{3}{5}\end{matrix}\right.\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=\dfrac{2m}{m^2-1}\)
\(\Leftrightarrow\left[{}\begin{matrix}x_2+2=0\\x_2+2=\dfrac{6}{5}:\left(\dfrac{36}{25}-1\right)=\dfrac{30}{11}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x_2=-2\\x_2=\dfrac{8}{11}\end{matrix}\right.\)
CM
8 tháng 6 2017
Đáp án B
sin 2 x + 5 π 2 − m cos x + 1 = 0 ⇔ c o s 2 x − m cos x + 1 = 0 ⇔ 2 c o s 2 x = m cos x ⇔ cos x = 0 cos x = m 2 ⇔ x = π 2 + k π cos x = m 2
Mà x ∈ 0 ; 4 π 3 ⇒ x = π 2 cos x = m 2 *
Để phương trình có đúng 3 nghiệm trên 0 ; 4 π 3 ⇔ * có 2 nghiệm thuộc 0 ; 4 π 3
⇔ − 1 < m 2 ≤ − 1 2 ⇔ − 2 < m ≤ − 1
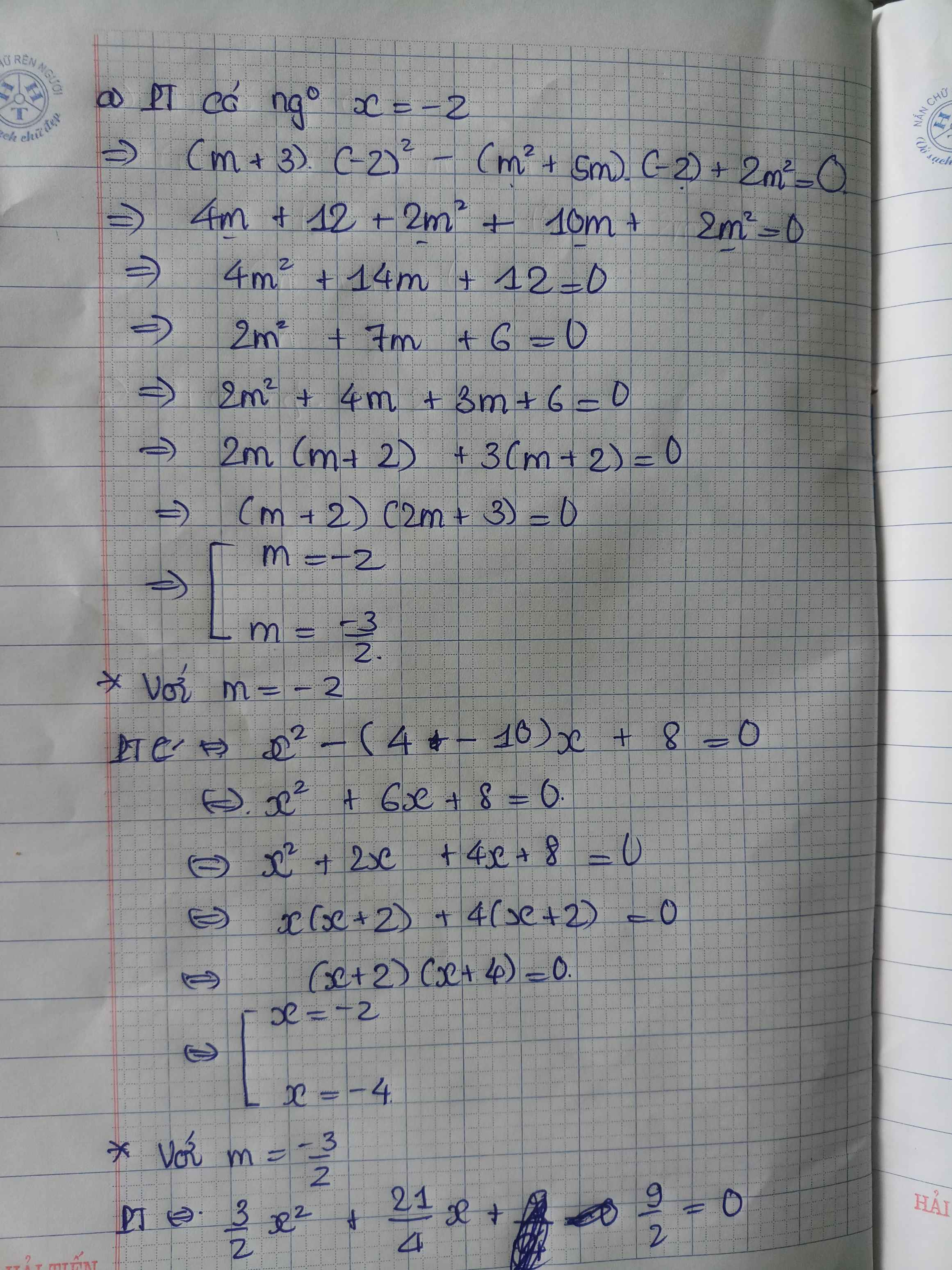
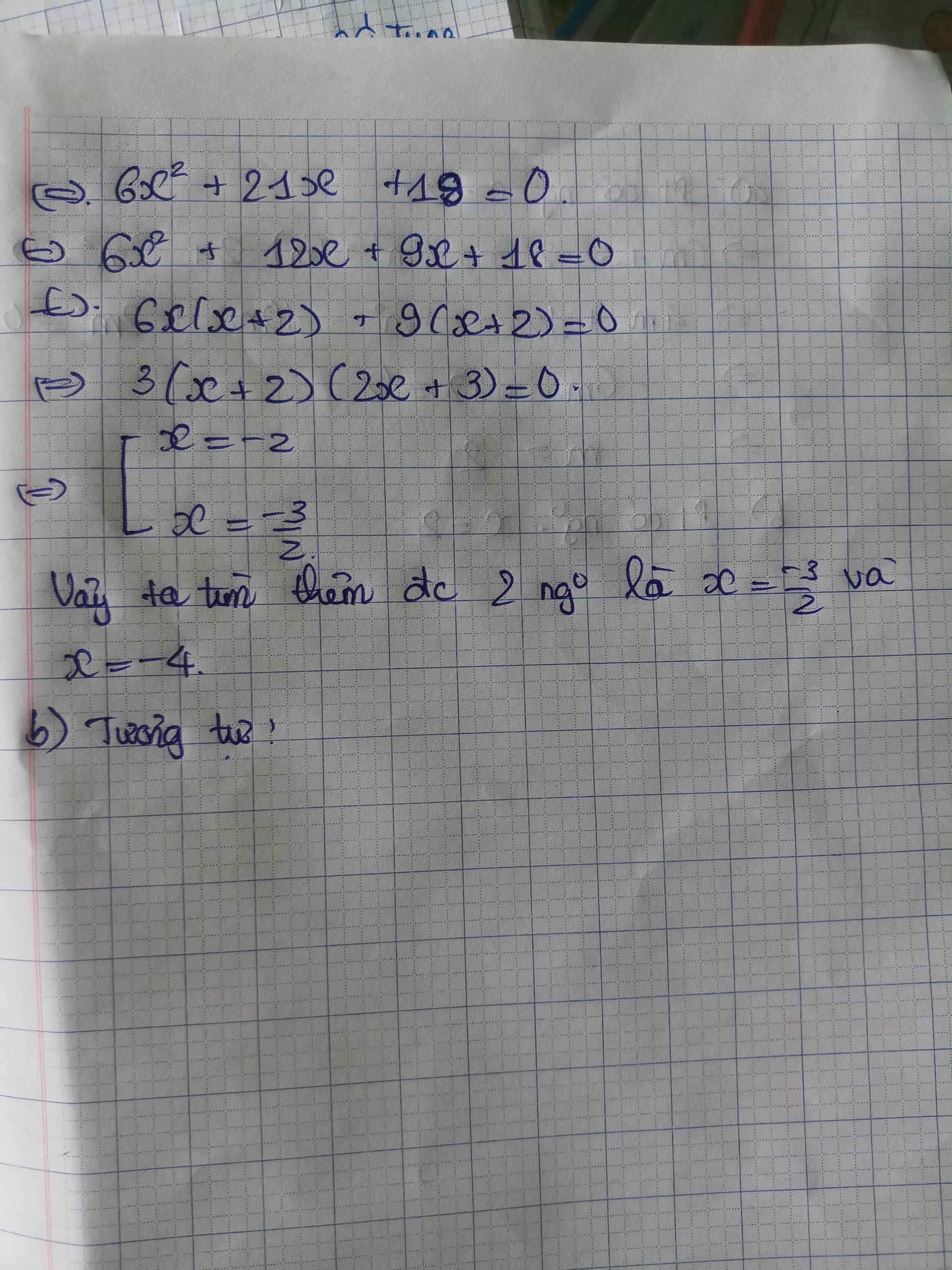
\(0\le x\le\frac{7\pi}{12}\Rightarrow0\le2x\le\frac{7\pi}{6}\)
\(\Rightarrow-\frac{1}{2}\le sin2x\le1\)
\(\Rightarrow-\frac{1}{2}\le7m+3\le1\)
\(\Rightarrow-\frac{1}{2}\le m\le-\frac{2}{7}\)
Cho hỏi là lúc nhân cho sin tại sao hai vế bên không có sin vâỵ