1, Cho hàm số y=\(\frac{x+1}{x^2+a}\) xác định a để tập giá trị của y chứa [0;1]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo:
a) Ta có: \(f(0) = a{.0^2} + b.0 + c = 1 \Rightarrow c = 1.\)
Lại có:
\(f(1) = a{.1^2} + b.1 + c = 2 \Rightarrow a + b + 1 = 2\)
\(f(2) = a{.2^2} + b.2 + c = 5 \Rightarrow 4a + 2b + 1 = 5\)
Từ đó ta có hệ phương trình \(\left\{ \begin{array}{l}a + b + 1 = 2\\4a + 2b + 1 = 5\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}a + b = 1\\4a + 2b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\end{array} \right.\)(thỏa mãn điều kiện \(a \ne 0\))
Vậy hàm số bậc hai đó là \(y = f(x) = {x^2} + 1\)
b) Tập giá trị \(T = \{ {x^2} + 1|x \in \mathbb{R}\} \)
Vì \({x^2} + 1 \ge 1\;\forall x \in \mathbb{R}\) nên \(T = [1; + \infty )\)
Đỉnh S có tọa độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - 0}}{{2.1}} = 0;{y_S} = f(0) = 1\)
Hay \(S\left( {0;1} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:

Hàm số nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\) và đồng biến trên khoảng \(\left( {0; + \infty } \right)\)

a) Tìm tập xác định của hàm số trên.
\(f\left( x \right)\) có nghĩa khi x0.
=> Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
b) Tính giá trị của hàm số khi \(x = - 1;x = 2022\)
Với \(x = - 1\), suy ta \(x < 0\)\( \Rightarrow y = - x = - \left( { - 1} \right) = 1\).
Với \(x = 2022\), suy ra \(x > 0\)\( \Rightarrow y = x = 2022\).

\(y=\dfrac{x^2-m^2+2m+1}{x-m}\) đúng không nhỉ?
\(y'=\dfrac{x^2-2mx+m^2-2m-1}{\left(x-m\right)^2}\)
Hàm đồng biến trên các khoảng xác định khi và chỉ khi:
\(x^2-2mx+m^2-2m-1\ge0\) ; \(\forall x\)
\(\Leftrightarrow\Delta'=m^2-\left(m^2-2m-1\right)\le0\)
\(\Leftrightarrow m\le-\dfrac{1}{2}\)

Điều kiện: m – 3 ≠ 0 ⇔ m ≠ 3
Đồ thị của hàm số y = (m – 3)x đi qua điểm A(1; 2) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có: 2 = (m – 3).1 ⇔ 2 = m – 3 ⇔ m = 5
Giá trị m = 5 thỏa mãn điều kiện bài toán.
Vậy với m = 5 thì đồ thị hàm sô y = (m – 3)x đi qua điểm A(1; 2).

Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
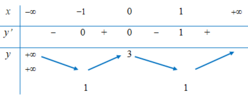
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.

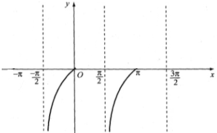
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
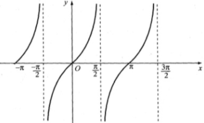
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
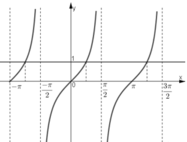
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
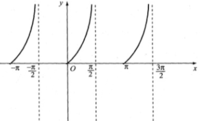
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
- Với \(a=-1\Rightarrow y=0\) vô nghiệm \(\Rightarrow\) miền giá trị của y ko chứa 0 (ko thỏa mãn)
- Với \(a< 0;a\ne-1\Rightarrow\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\sqrt{-a}^+}y=+\infty\\\lim\limits_{x\rightarrow\sqrt{-a}^-}y=-\infty\end{matrix}\right.\) \(\Rightarrow\) miền giá trị của y là R (thỏa mãn) (chính xác hơn là phải xét 2 TH \(a< -1\) và \(-1< a< 0\) )
- Với \(a=0\Rightarrow y'=\frac{-x^2-2x}{x^4}\Rightarrow y\ge y\left(-2\right)=-\frac{1}{4}\Rightarrow\) miền giá trị của y chứa [0;1] (thỏa mãn)
- Với \(a>0\)
Gọi m và M lần lượt là GTNN và GTLN của hàm số, để tập giá trị của y chứa \(\left[0;1\right]\) \(\Leftrightarrow\left\{{}\begin{matrix}m\le0\\M\ge1\end{matrix}\right.\)
\(y'=\frac{x^2+a-2x\left(x+1\right)}{\left(x^2+a\right)^2}=\frac{-x^2-2x+a}{\left(x^2+a\right)^2}\) luôn có 2 nghiệm pb trái dấu
\(-x^2-2x+a=0\Rightarrow\left(x+1\right)^2=a+1\Rightarrow\left[{}\begin{matrix}x_1=-1-\sqrt{a+1}\\x_2=-1+\sqrt{a+1}\end{matrix}\right.\)
\(x_1< -1\Rightarrow y\left(x_1\right)< 0\Rightarrow m< 0\); \(\forall a>0\)
Do đó ta chỉ cần tìm a để \(M\ge1\)
\(\Leftrightarrow y\left(x_2\right)\ge1\Leftrightarrow\frac{\sqrt{a+1}}{\left(-1+\sqrt{a+1}\right)^2+a}\ge1\)
\(\Leftrightarrow\sqrt{a+1}\ge2a+2-2\sqrt{a+1}\)
\(\Leftrightarrow3\sqrt{a+1}\ge2a+2\)
\(\Leftrightarrow-4a^2+a+5\ge0\)
\(\Rightarrow-1\le a\le\frac{5}{4}\)
Kết hợp lại, ta được \(\left\{{}\begin{matrix}a\le\frac{5}{4}\\a\ne-1\end{matrix}\right.\)
Mình cảm ơn nhiều.