bài 2 : giải phương trình:
| x - 2015 | + | 2x - 2016 | = x - 2017
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DS
0
AH
Akai Haruma
Giáo viên
14 tháng 10 2021
Lời giải:
a.
PT $\Leftrightarrow (x+3)^2=2016^{2020}-17^{91}+9$
Ta thấy: $2016^{2020}-17^{91}+9\equiv 0-(-1)^{91}+0\equiv -1\equiv 2\pmod 3$
Mà 1 scp thì chia $3$ chỉ dư $0$ hoặc $1$ nên pt vô nghiệm.
b.
$x^2=2016(y-1)^2-2017^{2019}\equiv 0-1^{2019}\equiv 3\pmod 4$
Mà 1 scp chia $4$ chỉ dư $0$ hoặc $1$ nên vô lý.
Vậy pt vô nghiệm.
c.
$(x-1)^2=2017^{2017}+1\equiv 1^{2017}+1\equiv 2\pmod 4$
Mà 1 scp khi chia cho $4$ chỉ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm
d.
$(x+2)^2=2018^{10}+4\equiv (-1)^{10}+1\equiv 2\pmod 3$
Mà 1 scp khi chia $3$ dư $0$ hoặc $1$ nên vô lý
Vậy pt vô nghiệm.
CL
5
MA
2 tháng 9 2016
\(\left|x-2015\right|^{2016}+\left|x-2016\right|^{2017}=1\)
Có: \(\left|x-2015\right|^{2016}\ge0;\left|x-2016\right|^{2017}\ge0\)
TH1: \(\hept{\begin{cases}\left|x-2015\right|^{2016}=1\\\left|x-2016\right|^{2017}=0\end{cases}}\Rightarrow\hept{\begin{cases}\left|x-2015\right|=1\\\left|x-2016\right|=0\end{cases}}\)
THa: \(x-2015=-1\Rightarrow x=2014\)
Thay vào: \(2014-2016\ne0\) ( loại)
THb: \(x-2015=1\Rightarrow x=2016\)
Thay vào: \(2016-2016=0\)( chọn )
TH2: \(\hept{\begin{cases}\left|x-2015\right|^{2016}=0\\\left|x-2016\right|^{2017}=1\end{cases}}\Rightarrow\hept{\begin{cases}\left|x-2015\right|=0\\\left|x-2016\right|=1\end{cases}}\)
THc: \(x-2016=-1\Rightarrow x=2015\)
Thay vào: \(2015-2015=0\)( chọn )
THd: \(x-2016=1\Rightarrow x=2017\)
Thay vào: \(2017-2015\ne0\)
Vậy: x = 2016 hoặc x = 2015
2 tháng 5 2016
Đặt 2x2+x-2015=a; x2-5x-2016=b
phương trình tương đương a2+4b2=4ab
=> a2-4ab+4b2=0
=> (a-2b)2=0
=> a=2b
vậy 2x2+x-2015=2*(x2-5x-2016)
=> x=\(\frac{-2017}{11}\)
5 tháng 10 2021
a, TK: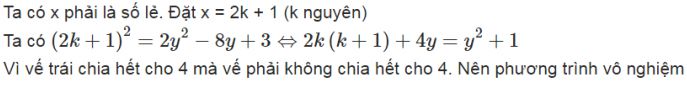
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2020
\(\Leftrightarrow\left(2x^2+x-2017\right)^2-4\left(2x^2+x-2017\right)\left(x^2-5x-2016\right)+4\left(x^2-5x-2016\right)^2=0\)
\(\Leftrightarrow\left(2x^2+x-2017-2\left(x^2-5x-2016\right)\right)^2=0\)
\(\Leftrightarrow11x-6049=0\)
\(\Rightarrow x=\frac{6049}{11}\)
6 tháng 10 2020
Xét: \(\sqrt{1+n^2+\frac{n^2}{\left(n+1\right)^2}}=\sqrt{\frac{\left(n+1\right)^2+n^2\left(n+1\right)^2+n^2}{\left(n+1\right)^2}}\) (với \(n\inℕ\))
\(=\sqrt{\frac{n^2+2n+1+n^4+2n^3+n^2+n^2}{\left(n+1\right)^2}}\)
\(=\sqrt{\frac{n^4+n^2+1+2n^3+2n^2+2n}{\left(n+1\right)^2}}\)
\(=\sqrt{\frac{\left(n^2+n+1\right)^2}{\left(n+1\right)^2}}=\frac{n^2+n+1}{n+1}=n+\frac{1}{n+1}\)
Áp dụng vào ta tính được: \(\sqrt{1+2015^2+\frac{2015^2}{2016^2}}+\frac{2015}{2016}=2015+\frac{1}{2016}+\frac{2015}{2016}\)
\(=2015+1=2016\)
Khi đó: \(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=2016\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=2016\)
Đến đây xét tiếp các TH nhé, ez rồi:))
TA
6 tháng 10 2020
chẳng biết đúng ko,mới lớp 5
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=\sqrt{1+2015^2+\frac{2015^2}{2016^2}}+\frac{2015}{2016}\)
\(\sqrt{x^2}-\sqrt{2x}+\sqrt{1}+\sqrt{x^2}-\sqrt{4x}+\sqrt{4}=\sqrt{1}+\sqrt{2015^2}+\sqrt{\frac{2015^2}{2016^2}}+\frac{2015}{2016}\)
\(\sqrt{x^2}-\sqrt{6x}+3=1+2015+\frac{2015}{2016}+\frac{2015}{2016}\)
\(x-\sqrt{6x}=1+\frac{2015}{1+2016+2016}-3\)
\(x-\sqrt{6x}=2-\frac{2015}{4033}\)
\(x-\sqrt{6x}=\frac{6051}{4033}\)
Ta có: |x-2015|+|2x-2016|=x-2017(*)
Trường hợp 1: x<1008
(*)\(\Leftrightarrow2015-x-2x+2016=x-1017\)
\(\Leftrightarrow4031-3x-x+1017=0\)
\(\Leftrightarrow5048-4x=0\)
\(\Leftrightarrow4x=5048\)
hay x=1262(loại)
Trường hợp 2: \(1008\le x< 2015\)
(*)\(\Leftrightarrow2015-x+2x-2016=x-2017\)
\(\Leftrightarrow x-1-x+2017=0\)
\(\Leftrightarrow2016=0\)(vô lý)
Trường hợp 3: \(x\ge2015\)
(*)\(\Leftrightarrow x-2015+2x-2016=x-2017\)
\(\Leftrightarrow3x-4031-x+2017=0\)
\(\Leftrightarrow2x-2014=0\)
\(\Leftrightarrow2x=2014\)
hay x=1007(loại)
Vậy: \(S=\varnothing\)
Ta thấy x - 2017 \(\ge\) 0 nên x \(\ge\) 2017.
Từ đó x - 2015 > 0; 2x - 2016 > 0.
Pt đã cho tương đương với:
x - 2015 + 2x - 2016 = x - 2017
\(\Leftrightarrow2x=2014\), vô lí vì 2x \(\ge\) 2017 . 2 > 2014.
Vậy pt đã cho vô nghiệm.