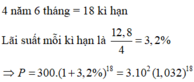ông T gửi tiết kiệm 200 triệu đồng vào ngân hàng A , kỳ hạn một năm. Cùng ngày , ông T gửi tiết kiệm 150 triệu đồng vào ngân hàng B , kỳ hạn một năm , với lãi suất cao hơn lãi suất của ngân hàng A là 1%/ năm . Biết sau đúng 1 năm kể từ ngày gửi tiền , ông T nhận được tổng số tiền lãi là 23,3 triệu đồng từ hai khoản tiền gửi tiết kiệm nêu trên. Hỏi lãi suất gửi tiết kiệm kỳ hạn 1 năm của ngân hàng A là bao nhiêu %?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi lãi suất tiết kiệm của ngân hàng A là x% (x>0)
Lãi suất của ngân hàng B: \(x+1\) %
Số tiền lãi bác nhận được từ ngân hàng A:
\(100.x\%=x\) (triệu đồng)
Số tiền lãi nhận được từ ngân hàng B:
\(150.\left(x+1\right)\%=1,5\left(x+1\right)\) (triệu)
Ta có pt:
\(x+1,5\left(x+1\right)=16,5\)
\(\Leftrightarrow x=6\) (%)

Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đ ồ n g .
Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đồng .

Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 24 % 4 ≈ 59.895.767 đồng
Đáp án D
Số tiền mà ông An nhận được là
T = 50.10 6 . 1 + 8 , 4 4 % 3 . 1 + 12 4 % 4 ≈ 59.895.767 đ ồ n g .

Áp dụng công thức lãi kép: ![]()
Như vậy, khi gửi không kỳ hạn để được số tiền gồm cả vốn lẫn lãi lớn hơn hoặc bằng 300 triệu đồng thì ông A phải gửi tối thiểu là 100 tháng.
Nếu cũng gửi với số tiền ban đầu là 300 triệu đồng với lãi suất 1,2%/quý trong thời gian 100 năm (gồm 33 kỳ hạn và 1 tháng không kỳ hạn)
• Số tiền ông A có được sau định kỳ là: ![]()
• Số tiền ông A có được sau 100 tháng là
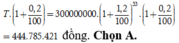

Đáp án C
Gọi A là số tiền gốc ban đầu, lãi suất r / năm, số tiền gửi thêm là a (triệu đồng).
Sau năm đầu tiên, số tiền cả gốc lẫn lãi mà ông Minh nhận được là: A 1 + r
Sau năm thứ 2, cả gốc và lãi ông nhận được là: A 1 + r + a 1 + r = A 1 + r 2 + a 1 + r
Sau năm thứ 3, cả gốc và lãi ông nhận được:
A 1 + r 2 + a 1 + r + a 1 + r = A 1 + r 3 + a 1 + r 2 + a 1 + r
…
Sau năm thứ n, ông Minh nhận được số tiền:
A 1 + r n + a 1 + r n − 1 + a 1 + r n − 2 + . .. + a = A 1 + r n + a . 1 + r n − 1 r
Thay số: sau 10 năm ông Minh nhận về cả gốc lẫn lãi là
200 1 + 0 , 07 10 + 20. 1 + 0 , 07 10 − 1 0 , 07 = 669 , 759 triệu đồng.

Gọi lãi suất của ngân hàng đó trong 1 năm là x(%)(ĐK: x>0)
Sau 1 năm thì số tiền bác Ba nhận được sẽ là;
\(500000000\left(1+0,01x\right)\left(đồng\right)\)
Sau 2 năm thì số tiền bác Ba nhận được sẽ là:
\(500000000\left(1+0,01x\right)^2\)(đồng)
Theo đề, ta có:
\(500000000\left(1+0,01x\right)^2=574592000\)
=>\(\left(1+0,01x\right)^2=1,149184\)
=>\(1+0,01x=1,072\)
=>0,01x=0,072
=>x=7,2(nhận)
Vậy: Lãi suất của ngân hàng là 7,2%/năm