Question

[Thiên Thần ( Fire Smoke Team )]

Cho hình thoi ABCD có cạnh bằng 12,5cm, đường cao bằng 6,72cm và AC<BD. Độ dài hai đường chéo AC và BD lần lượt là...?

Answer 1

[Ngoc Han ♪]

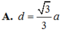
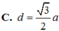
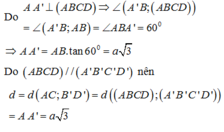
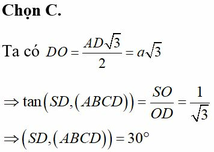
Ta có:

\(S_{ABCD}=12,5\times6,72=84\) ( cm² )

Gọi độ dài hai đường chéo hình thoi là \(a\) và \(b\) ( a > b > 0 )

Khi đó :

\(\frac{1}{a}ab=84\)

\(\Leftrightarrow2ab=336\)

Gọi giao điểm 2 đường chéo là O .

Vì ABCD là hình thoi nên AC vuông góc BD

\(\Rightarrow\) Tam giác AOB vuông tại O

\(\Rightarrow\)\(AB^2=OA^2+OB^2\)

Mà \(OA=\frac{1}{2}b;OB=\frac{1}{2}a\)( Do tứ giác ABCDABCD là hình thoi )

Nên \(\frac{1}{4}\left(a^2+b^2\right)=12,5^2\)

\(\Leftrightarrow a^2+b^2=625\)

Ta có:

∙\(\hept{\begin{cases}a^2+b^2=625\Leftrightarrow a^2+b^2+2ab=625+336\Leftrightarrow\left(a+b\right)^2=961\Leftrightarrow a+b=31\\a^2+b^2=625\Leftrightarrow a^2+b^2-2ab=625-336\Leftrightarrow\left(a-b\right)^2=289\Leftrightarrow a-b=17\end{cases}}\)

Từ đó tính được \(a=24;b=7\)