Cho sin2x = 3/4 . Tính tanx+ cotx
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TH
1
CM
11 tháng 12 2017
Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài ra cũng có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t.
Cách 1: Điều kiện của phương trình:
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ -1 (1)
Ta có:
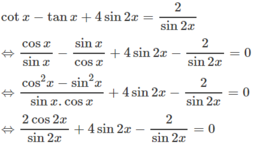
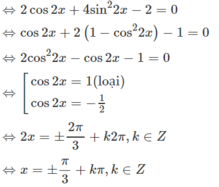
Cách 2. Đặt t = tanx
Điều kiện t ≠ 0
Phương trình đã cho có dạng
PT
1
CM
23 tháng 4 2017
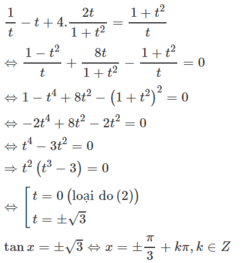
Điều kiện của phương trình: sinx ≠ 0, cos ≠ 0, tan ≠ -1.
Biến đổi tương đương đã cho, ta được
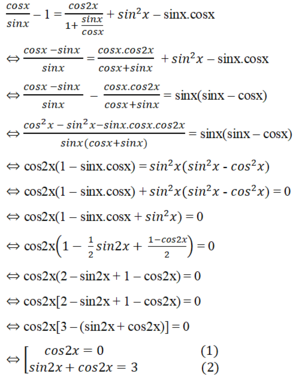
Phương trình (2) vô nghiệm vì |sin2x + cos2x| ≥ √2.
Phương trình (1) có nghiệm 2x = π/2+kπ,k ∈ Z
⇒ x = π/4+ k π/2,k ∈ Z.
Giá trị x = π/4+ k π/2, k = 2n + 1,
với n ∈ Z bị loại do điều kiện tanx ≠ -1.
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 8 2020
ĐKXĐ: \(sin2x\ne0\)
\(\Leftrightarrow\frac{cos^2x-sin^2x}{sinx.cosx}+4sin2x=\frac{2}{sin2x}\)
\(\Leftrightarrow\frac{2cos2x}{sin2x}+4sin2x=\frac{2}{sin2x}\)
\(\Leftrightarrow cos2x+2sin^22x=1\)
\(\Leftrightarrow cos2x-2\left(1-cos^22x\right)-1=0\)
\(\Leftrightarrow2cos^22x+cos2x-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=1\left(ktm\right)\\cos2x=-\frac{3}{2}>1\left(l\right)\end{matrix}\right.\)
Phương trình vô nghiệm
PD
1
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 8 2020
ĐKXĐ: \(\left\{{}\begin{matrix}sin2x\ne0\\tanx\ne-1\end{matrix}\right.\)
\(\frac{cosx}{sinx}-1=\frac{cos^2x-sin^2x}{1+\frac{sinx}{cosx}}+sin^2x-sinx.cosx\)
\(\Leftrightarrow\frac{cosx-sinx}{sinx}=cosx\left(cosx-sinx\right)-sinx\left(cosx-sinx\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx-sinx=0\Rightarrow x=\frac{\pi}{4}+k\pi\\\frac{1}{sinx}=cosx-sinx\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow sinx.cosx-sin^2x=1\)
\(\Leftrightarrow2sinx.cosx+1-2sin^2x=3\)
\(\Leftrightarrow sin2x+cos2x=3\)
Vế trái không lớn hơn 2 nên pt vô nghiệm
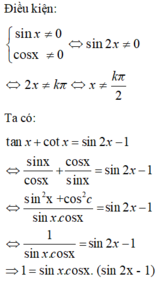
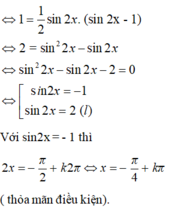
cái này bạn có thể tính nhanh bằng cách sử dụng máy tính
+, B1 bạn ấn shift sin để tìm giá trị 2x -> x
+, B2 ấn shift RCL xong ấn A để gắn biến
+ B3 bạn nhập biểu thức : tan A + 1 / tan A vào
và mình tính nó ra 8/3
Chúc bạn học tốt nha
#mã mã#
Cảm ơn bn nha