Từ điểm A nằm ngoài (O), kẻ hai tiếp tuyến AB, AC với (O) (B, C là tiếp điểm)
a) Chứng minh tứ giác ABOC nội tiếp. Xác định tâm của đường tròn,
b) Gọi D là trung điểm của đoạn AC. Đoạn thẳng BD cắt (O) tại E. Tia AE cắt (O) tại F.
c) Gọi H là giao điểm của OA và BC. CM: \(\widehat{DHC}\) = \(\widehat{DEC}\)




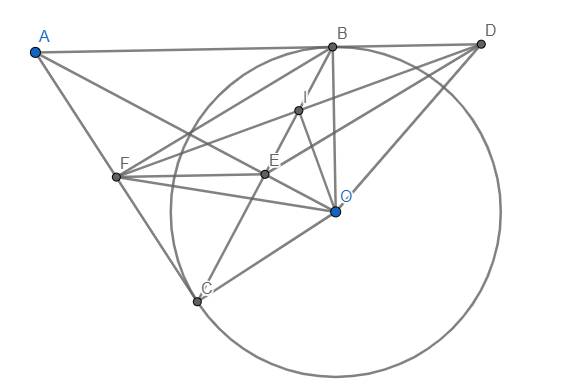
à câu b chứng minh \(AB^2=AE.AF\)
giúp mik câu c vs
câu b hình như thiếu thì phải viết đề bài đủ nha bạn