Cho đường tròn (C): x2+y2+4x+2y+4=0 và điểm A(m; 2-m). Với giá trị nào của m thì qua A kẻ được hai tiếp tuyến tới đường tròn tạo với nhau một góc 60 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 7 2018
x 2 + y 2 + 4 x − 2 y − 4 = 0 và điểm M(-2; 4)
Đường tròn (C): x 2 + y 2 + 4 x - 2 y - 4 = 0 có tâm I(-2;1) và bán kính R = ( − 2 ) 2 + 1 2 + 4 = 3
Phương trình tiếp tuyến tại M(- 2; 4) và nhận I M → ( 0 ; 3 ) làm VTPT là:
0( x +2) + 3 (y – 4) = 0 hay y = 4
ĐÁP ÁN D
CM
15 tháng 11 2019
Đường tròn (C): x 2 + y 2 + 4 x − 2 y − 4 = 0 có tâm I(-2; 1) và bán kính R = 3.
Ta có : I M = 1 + 2 2 + 2 − 1 2 = 10 > 3 nên M nằm ngoài đường tròn.
Qua M kẻ được hai tiếp tuyến đến đường tròn.
ĐÁP ÁN C
CM
16 tháng 1 2017
ĐÁP ÁN B
Đường tròn (C): x 2 + y 2 - 4 x + 2 y – 4 = 0 có tâm I(2; -1) và bán kính R = 2 2 + ( − 1 ) 2 + 4 = 3
Tiếp tuyến qua M( -4; 2) và nhận n → ( a ; b ) làm VTPT có phương trình :
a( x+ 4) + b (y – 2)= 0 hay ax + by + 4a – 2b = 0 (*)
Khoảng cách từ tâm I đến tiếp tuyến bằng bán kính nên ta có:
d ( I ; d ) = R ⇔ 2 a − b + 4 a − 2 b a 2 + b 2 = 3 ⇔ 6 a − 3 b a 2 + b 2 = 3 ⇔ 2 a − b a 2 + b 2 = 1 ⇔ 2 a − b = a 2 + b 2 ⇔ 4 a 2 − 4 a b + b 2 = a 2 + b 2 ⇔ 3 a 2 − 4 a b = 0 ⇔ a ( 3 a − 4 b ) = 0 ⇔ a = 0 3 a = 4 b
* Nếu a= 0 , chọn b= 1 thay vào (*) ta có phương trình tiếp tuyến là: y – 2= 0
* Nếu 3a = 4b, chọn a = 4 thì b = 3 thay vào (*) ta có phương trình tiếp tuyến là:
4x + 3y + 10 = 0
Vậy có 2 tiếp tuyến qua M là: y – 2= 0 và 4x +3y + 10= 0
28 tháng 3 2023
(C): x^2+y^2+4x-2y-4=0
=>(x+2)^2+(y-1)^2=9
=>I(-2;1); R=3
M thuộc d nên M(a;1-a)
M nằm ngoài (C) nên IM>R
=>IM^2>9
=>2a^2+4a-5>0
MA^2=MB^2=IM^2-IA^2=(a+2)^2+(-a)^2-9=2a^2+4a-5
=>x^2+y^2-2ax+2(a-1)y-6a+6=0(1)
A,B thuộc (C)
=>Tọa độ A,B thỏa mãn phương trình:
x^2+y^2+4x-2y-4=0(2)
(1)-(2)=(a+2)x-ay+3a-5=0(3)
Tọa độ A,B thỏa mãn (3) nên (3) chính là phương trình đường thẳng AB
(E) tiếp xúc AB nên (E): R1=d(E,AB)
Chu vi của (E) lớn nhất khi R1 lớn nhất
=>d(E;AB) lớn nhất
Gọi H là hình chiếu vuông góc của E lên AB
=>d(E,Δ)=EH<=EK=căn 10/2
Dấu = xảy ra khi H trùng K
=>AB vuông góc EK
vecto EK=(-1/2;3/2), AB có VTCP là (a;a+2)
AB vuông góc EK
=>-1/2a+3/2(a+2)=0
=>a=-3
=>M(-3;4)
CM
30 tháng 11 2019
Đáp án D
Gọi d là đường thẳng qua M có véc tơ chỉ phương:
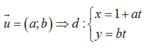
- Đường tròn (C1) tâm I1 (1;1) và R1= 1
Đường tròn (C2) : tâm I2( -2;0) và R2= 3
- Nếu d cắt (C1) tại A :
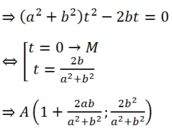
- Nếu d cắt (C2) tại B:
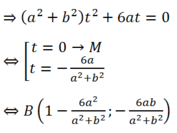
- Theo giả thiết: MA= 2 MB nên MA2= 4 MB2 (*)
- Ta có :
CM
31 tháng 10 2017
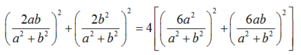
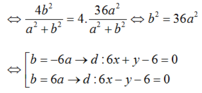
Đường tròn (C): x 2 + y 2 + 4 x + 2 y + 4 = 0 có tâm I(-2;-1) và bán kính R = 1.
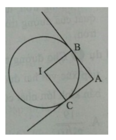
Gọi 2 tiếp điểm là B và C.
Ta có: B A C ^ = 60 0 nên B A I ^ = I A C ^ = 1 2 B A C ^ = 30 0 ( tính chất 2 tiếp tuyến cắt nhau).
Vì sin B A I ^ = sin 30 0 = 1 2 ; lại có: sin B A I ^ = B I A I = R A I
Suy ra: R A I = 1 2 ⇔ A I = 2 R = 2 ( vì R = 1)
⇔ m + 2 2 + 3 − m 2 = 2 2 ⇒ 2 m 2 − 2 m + 9 = 0 (vô nghiệm).
Chọn D.
CM
7 tháng 1 2019
Qua điểm A(m ; m + 2) có hai tiếp tuyến với (C) khi và chỉ khi A nằm ngoài (C)
⟺ m 2 + m + 2 2 + 4 m − 2 m − 4 > 0 ⇒ 2 m 2 + 6 m > 0 ⇒ m > 0 m < − 3
Chọn D
CM
3 tháng 9 2017
(C): x 2 + y 2 − 4 x + 2 y − 15 = 0 và đường thẳng ∆: - 4x + 3y + 1 = 0.
Đường tròn (C): x 2 + y 2 − 4 x + 2 y − 15 = 0 có tâm I(2; -1) và bán kính R = 20 .
Khoảng cách d I , ∆ = − 4.2 + 3. − 1 + 1 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm phân biệt A, B cách nhau một khoảng là
A B = 2 R 2 − d I , ∆ 2 = 8 .
ĐÁP ÁN C
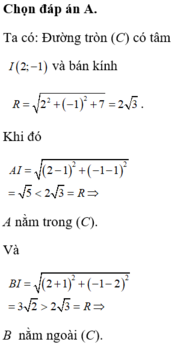
Đường tròn (C) tâm \(I\left(-2;-1\right)\) bán kính \(R=1\)
\(\overrightarrow{IM}=\left(m+2;3-m\right)\Rightarrow IM^2=\left(m+2\right)^2+\left(3-m\right)^2=2m^2-2m+13\)
Giả sử A nằm ngoài đường tròn và 2 tiếp điểm là B và C
\(\Rightarrow\widehat{BAC}=60^0\Rightarrow\widehat{IAB}=30^0\)
\(\Rightarrow IM=\frac{IB}{sin30^0}=2IB=2R=2\Rightarrow IM^2=4\)
\(\Rightarrow2m^2-2m+13=4\Leftrightarrow2m^2-2m+9=0\) (vô nghiệm)
Ko tồn tại m thỏa mãn
Bạn xem lại đề, điểm M nằm quá xa đường tròn (M thuộc \(x+y-2=0\) ) nên góc chắc chắn là rất nhỏ