viết các thủ tục và hàm xử lí các công việc sau :
a, tính n!
b, tìm giá trị lớn nhất của 2 số a,b
c, hoán đổi giá trị 2 số a, b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

```
def tong_tu_1_den_n(n):
tong = 0
for i in range(1, n+1):
tong += i
return tong
```
Hàm này sử dụng vòng lặp for để tính tổng của các số từ 1 đến n. Ban đầu, ta khởi tạo biến tong bằng 0. Sau đó, ta lặp qua các số từ 1 đến n và cộng chúng vào biến tong. Cuối cùng, ta trả về giá trị của biến tong.
Viết thủ tục thực hiện việc hoán đổi hai giá trị của a và b:```
def hoan_doi(a, b):
temp = a
a = b
b = temp
return a, b
```
Thủ tục này sử dụng biến tạm temp để lưu giá trị của a trước khi hoán đổi. Sau đó, ta gán giá trị của b cho a và giá trị của temp (tức là giá trị ban đầu của a) cho b. Cuối cùng, ta trả về hai giá trị đã được hoán đổi.

1)
uses crt;
var a,b,bcnn,i:integer;
begin
clrscr;
write('a='); readln(a);
write('b='); readln(b);
bcnn:=a*b;
for i:=a*b-1 downto 1 do
if (i mod a=0) and (i mod b=0) then
begin
if bcnn>i then bcnn:=i;
end;
writeln(bcnn);
readln;
end.
2:
procedure hoandoi(a,b:integer);
var tam:integer;
begin
tam:=a;
a:=b;
b:=tam;
end;

1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)

1: Hoán đổi giá trị hai biến x và y
Chúng ta sẽ gán biến trung gian tam cho x, xong rồi gán biến trung gian tam đó cho y; rồi sau đó gán y ngược lại cho x, và xuất kết quả ra-đó chính là x và y sau khi hoán đổi cho nhau.
2: Tìm giá trị lớn nhất của dãy A
Chúng ta sẽ gán biến ln cho a[1], sau đó sẽ quét qua các phần tử trong mảng xem thử có phần tử nào lớn hơn ln thì gán ln cho phần tử đó. Sau cùng xuất ln ra, ta được số lớn nhất cần tìm.

Đáp án A.

Mệnh đề 3 sai ví dụ hàm số y=|x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó.
Mệnh đề 4 đúng vì nếu hàm số y=f(x) có đạo hàm trên [a;b] thì hàm số liên tục trên [a;b] do đó hàm số có nguyên hàm trên [a;b]

a) 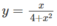 trên khoảng (−
∞
;+
∞
);
trên khoảng (−
∞
;+
∞
);
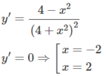
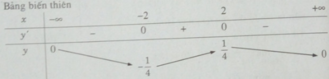
Từ đó ta có min f(x) = −1/4; max f(x) = 1/4
b) 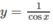 trên khoảng
trên khoảng 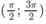
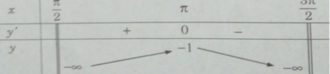
y′ = 0 ⇔ x = π
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y(π) = −1.

2:
#include <bits/stdc++.h>
using namespace std;
double xm,ix,iy,r,ma,mb;
int main()
{
cin>>ix>>iy;
cin>>r;
cin>>ma>>mb;
xm=sqrt((ix-ma)*(ix-ma)+(iy-mb)*(iy-mb));
if (xm==r) cout<<"phai";
else cout<<"khong phai";
return 0;
}
a)
*Hàm
function giaithua(n:integer):longint;
var i:integer;
begin
giaithua:=1;
for i:=1 to n do
giaithua:=giaithua*i;
end;
b)
*Hàm
function max(a,b:integer):integer;
begin
max:=a;
if max<b then max:=b;
end;
c)
*Thủ tục
procedure hoandoi(a,b:integer);
var tam:integer;
begin
begin
tam:=a;
a:=b;
b:=tam;
end;
end;