Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(R=\rho\dfrac{l}{S}\Rightarrow S=\dfrac{\rho.l}{R}=\dfrac{1,1.10^{-6}.0,8}{4,5}\approx1,9\left(5\right).10^{-7}\left(m^2\right)\)
\(S=\pi\dfrac{d^2}{4}\Rightarrow d=\sqrt{\dfrac{4S}{\pi}}=\sqrt{\dfrac{4.1,9\left(5\right).10^{-7}}{\pi}}\approx5.10^{-4}\left(m\right)=0,5\left(mm\right)\)
\(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,1.10^{-6}.0,8}{4,5}=1,9.10^{-7}\left(m^2\right)\)
\(S=\pi\dfrac{d^2}{4}\Rightarrow d^2=\dfrac{4S}{\pi}=\dfrac{4.1,9.10^{-7}}{\pi}\simeq2,42.10^{-7}\)
\(\Rightarrow d=\sqrt{2,42.10^{-7}}.10000\simeq0,5\left(mm\right)\)
Chọn D
Áp dụng công thức tính R: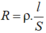 
Trong đó tiết diện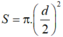 
(d là đường kính tiết diện)
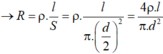
→ Đường kính tiết diện của dây nung là:
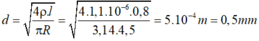
\(R=\rho\dfrac{l}{S}\Rightarrow l=\dfrac{R.S}{\rho}=\dfrac{1,1.1,2.10^{-6}}{1,1.10^{-6}}=1,2\left(m\right)\Rightarrow D\)
a. \(R=p\dfrac{l}{S}=1,1\cdot10^{-6}\dfrac{3}{0,05\cdot10^{-6}}=66\Omega\)
b. \(\left\{{}\begin{matrix}P=\dfrac{U^2}{R}=\dfrac{220^2}{66}\approx733,\left(3\right)\left(W\right)\\Q_{toa}=A=UIt=220\cdot\dfrac{220}{66}\cdot30\cdot60=1320000\left(J\right)\end{matrix}\right.\)
+)Đường kính của dây là
d
1
= 0,6mm, suy ra tiết diện dây là: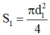 
+)Đường kính dây giảm xuống còn
d
2
= 0,4mm, suy ra tiết diện dây là: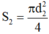 
Áp dụng kết quả thu được từ bài 8.11 ta có: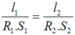 
Thay R 1 = R 2 (vì không thay đổi điện trở của dây nung) ta được:
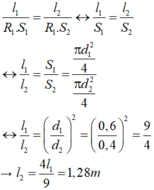
\(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,1.10^{-6}.1,6}{9}\simeq2.10^{-7}\left(m^2\right)\)
\(S=\pi\dfrac{d^2}{4}\Rightarrow d^2=\dfrac{4S}{\pi}=\dfrac{4.2.10^{-7}}{\pi}\simeq2,5.10^{-7}\)
\(\Rightarrow d=\sqrt{2,5.10^{-7}}.1000=0,5\left(mm\right)\)