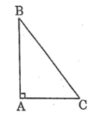
Cho tam giác ABC vuông tại A,AB<AC,.Tia phân giác của góc ABC cát ACtại D.Qua C kẻ đg thg vuông goc vs Ac cắt BD tại E.C/m CE>AC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
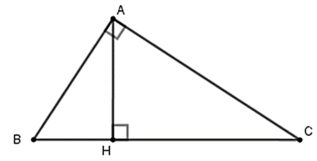
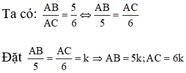
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:


Ta có: A B A C = 3 7 ⇒ A B = 3 7 A C
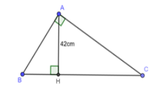
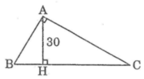
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
1 A H 2 = 1 A B 2 + 1 A C 2 ⇔ 1 42 2 = 49 9 A C 2 + 1 A C 2 ⇔ 1 42 2 = 58 9 A C 2 ⇔ A C 2 = 11369
AC = 14 58 (cm) AB = 3 7 . 14 58 = 6 58 (cm)
Áp dụng định lý Pytago cho ABH vuông tại A có: A B 2 + A C 2 = B C 2
⇔ B C 2 = 6 58 2 + 14 58 2 ⇔ B C 2 = 13456 ⇒ B C = 116 c m
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
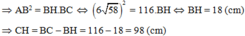
Đáp án cần chọn là: A

a: Xet ΔBAC vuông tại B và ΔHAB vuông tại H có
góc A chung
=>ΔBAC đồng dạng với ΔHAB
\(S_{BAC}=\dfrac{1}{2}\cdot9\cdot12=54\left(cm^2\right)\)
b: \(AC=\sqrt{9^2+12^2}=15\left(cm\right)\)
BH=9*12:15=108/15=7,2(cm)
c: \(S_{ABC}=\dfrac{1}{2}\cdot BA\cdot BC=\dfrac{1}{2}\cdot BH\cdot AC\)
=>BA*BC=BH*AC

Sửa đề: Đường cao AK
a: Sửa đề: Chứng minh ΔBKA~ΔBAC và \(BA^2=BK\cdot BC\)
Xét ΔBKA vuông tại K và ΔBAC vuông tại A có
\(\widehat{KBA}\) chung
Do đó: ΔBKA~ΔBAC
=>\(\dfrac{BK}{BA}=\dfrac{BA}{BC}\)
=>\(BA^2=BK\cdot BC\)
b: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=17^2-8^2=225=15^2\)
=>AC=15(cm)
Xét ΔBAC có BM là phân giác
nên \(\dfrac{AM}{AB}=\dfrac{CM}{CB}\)
=>\(\dfrac{AM}{8}=\dfrac{CM}{17}\)
mà AM+CM=AC=15
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AM}{8}=\dfrac{CM}{17}=\dfrac{AM+CM}{8+17}=\dfrac{15}{25}=0,6\)
=>\(AM=0,6\cdot8=4,8\left(cm\right);CM=17\cdot0,6=10,2\left(cm\right)\)
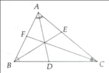
c: Sửa đề: Chứng minh \(\widehat{BNK}=\widehat{BMA}\)
Ta có: \(\widehat{BNK}+\widehat{KBN}=90^0\)(ΔNKB vuông tại K)
\(\widehat{BMA}+\widehat{ABM}=90^0\)(ΔAMB vuông tại A)
mà \(\widehat{KBN}=\widehat{ABM}\)
nên \(\widehat{BNK}=\widehat{BMA}\)



câu hỏi đâu bạn