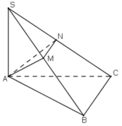
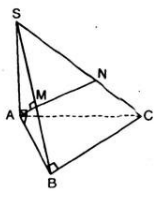
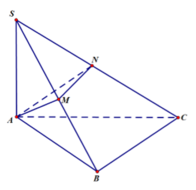
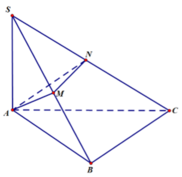
Cho tứ diện SABC có SA ⊥ (ABC), tam giác ABC vuông tại B. Trong mặt phẳng SAB kẻ AM vuông góc với SB tại M, trên cạnh SC lấy điểm N sao cho SN/SC= SM/SB.
a, CMR BC ⊥(SAB); AM⊥(SBC) ; SB⊥AN
b, Biết SA = a√2 ; AB=BC=a, tính diện tichs tam giác AMN
c, H là hình chiếu của A lên SC, K là giao điểm của HM với (ABC). CMR AK⊥AC


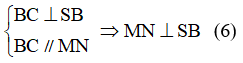
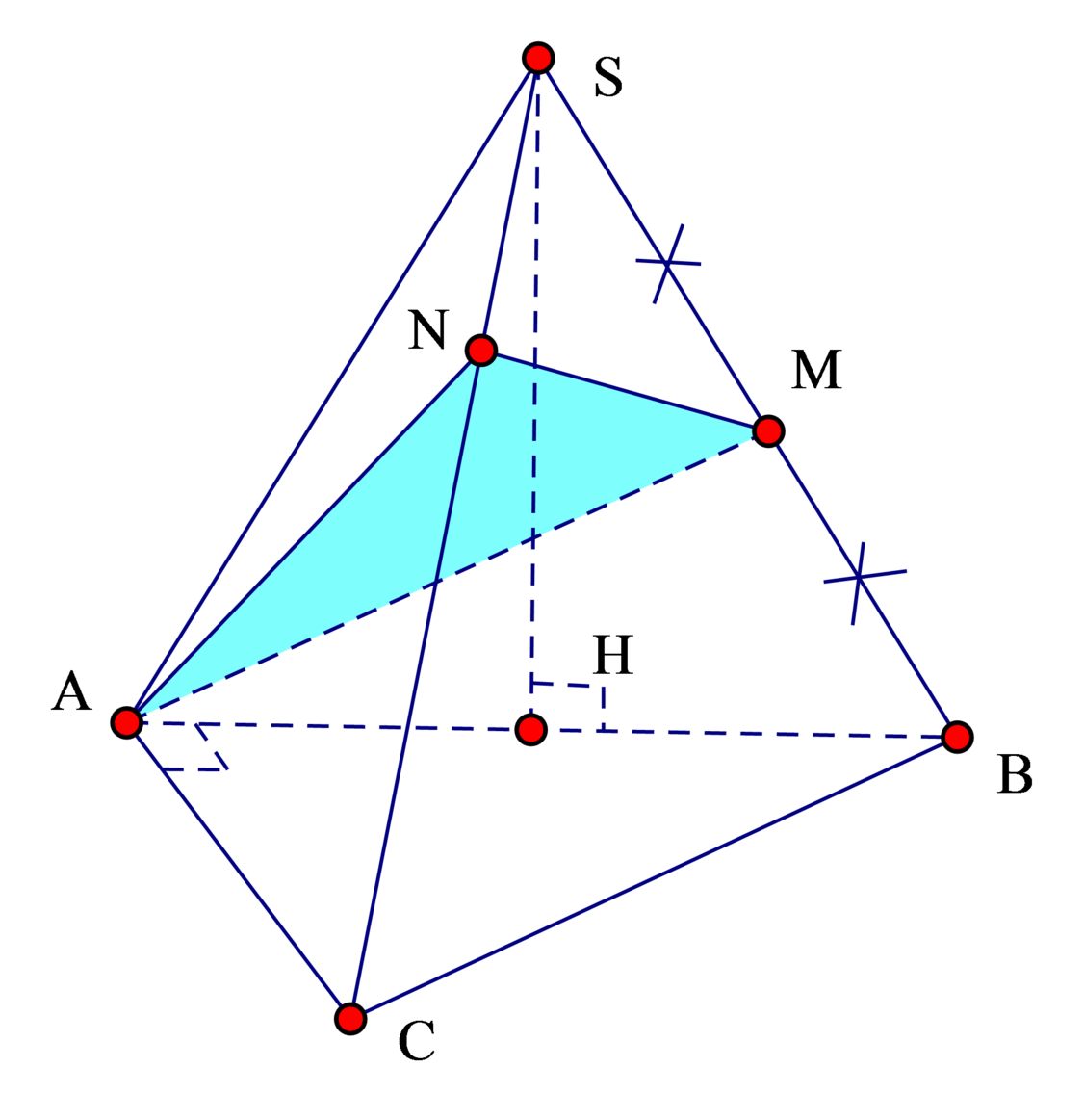
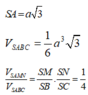
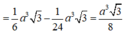
Trong mặt phẳng (SBC), nối HM kéo dài cắt BC tại K \(\Rightarrow AK\in\left(ABC\right)\)
Từ câu a có \(AM\perp\left(SBC\right)\) \(\Rightarrow AM\perp SC\)
Mà \(SC\perp AH\Rightarrow SC\perp\left(AHM\right)\Rightarrow SC\perp AK\) (1)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SAC\right)\Rightarrow AK\perp AC\)