giúp b2 hoặc b3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\widehat{B}_1=\widehat{B_3}\) đối đỉnh
\(\widehat{A}_1=\widehat{B}_1\) theo bài đầu
Do đó \(\widehat{A_1}=\widehat{B_3}\)
Mặt khác,ta có \(\widehat{A_1}+\widehat{A_4}=180^0\) hai góc kề bù
=> \(\widehat{A_4}=180^0-\widehat{A_1}\) \((1)\)
Và \(\widehat{B_2}+\widehat{B_3}=180^0\) hai góc kề bù
=> \(\widehat{B_2}=180^0-\widehat{B_3}\) \((2)\)
\(\widehat{A_1}=\widehat{B_3}\) \((3)\)
Từ 1,2,3 ta có : \(\widehat{A_4}=\widehat{B_2}\)
b, \(\widehat{A_2}=\widehat{A_4}\) đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) theo câu a
Do đó : \(\widehat{A_2}=\widehat{B_2};\widehat{A_1}=\widehat{A_3}\) đối đỉnh
\(\widehat{A_1}=\widehat{B_3}\) câu a
Do đó \(\widehat{A_3}=\widehat{B_3}\). Mặt khác \(\widehat{B_2}=\widehat{B_4}\) hai góc đối đỉnh
\(\widehat{A_4}=\widehat{B_2}\) câu a . Do đó \(\widehat{A_4}=\widehat{B_4}\)
c, \(\widehat{B_1}+\widehat{B_2}=180^0\) hai góc kề bù
\(\widehat{A_1}=\widehat{B_1}\) theo đầu bài
Do đó \(\widehat{A_1}+\widehat{B_2}=180^0\)
Mặt khác \(\widehat{B_2}+\widehat{B_3}=180^0\) kề bù
\(\widehat{A_4}=\widehat{B_2}\) theo câu a . Do đó \(\widehat{A_4}+\widehat{B_3}=180^0\)

Bài 2:
a: Để (d)//(d') thì \(m=2m+1\)
\(\Leftrightarrow-m=1\)
hay m=-1
c: Để (d) cắt (d') thì \(m\ne2m+1\)
hay \(m\ne-1\)

\(2,\\ 1,=20\sqrt{3}+20\sqrt{3}+\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}=40\sqrt{3}+\sqrt{3}=41\sqrt{3}\\ 2,A=\dfrac{2\sqrt{x}-9-x+9+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ A=\dfrac{2\sqrt{x}-x+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\\ c,A< 1\Leftrightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-1< 0\\ \Leftrightarrow\dfrac{4}{\sqrt{x}-3}< 0\Leftrightarrow\sqrt{x}-3< 0\left(4>0\right)\\ \Leftrightarrow x< 9\Leftrightarrow0\le x< 9\)
\(3,\\ 1,A=\sqrt{2}-1-\dfrac{\sqrt{2}\left(2-\sqrt{5}\right)}{2-\sqrt{5}}=\sqrt{2}-1-\sqrt{2}=-1\\ 2,\\ a,P=\dfrac{\sqrt{x}+2-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\left(\sqrt{x}+2\right)^2}{4}\left(x\ge0;x\ne4\right)\\ P=\dfrac{4\left(\sqrt{x}+2\right)}{4\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\\ b,P< 1\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-2}-1< 0\\ \Leftrightarrow\dfrac{4}{\sqrt{x}-2}< 0\Leftrightarrow\sqrt{x}-2< 0\left(4>0\right)\\ \Leftrightarrow x< 4\Leftrightarrow0\le x< 4\)

2.
a.
\(P=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2\left(x+5\right)}{\left(x-5\right)\left(x+5\right)}\)
\(=\dfrac{1}{x+5}+\dfrac{2}{x-5}-\dfrac{2}{x-5}=\dfrac{1}{x+5}\)
b.
\(P=-3\Rightarrow\dfrac{1}{x+5}=-3\Rightarrow x+5=-\dfrac{1}{3}\)
\(\Rightarrow x=-\dfrac{16}{3}\)
Thay vào bấm máy ta được \(Q=529\)
3.
a. \(P=\dfrac{3\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}+\dfrac{18}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{3\left(x-3\right)+x+3+18}{\left(x-3\right)\left(x+3\right)}=\dfrac{4x+12}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{4\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{4}{x-3}\)
b.
\(P=4\Rightarrow\dfrac{4}{x-3}=4\Rightarrow x-3=1\)
\(\Rightarrow x=4\)

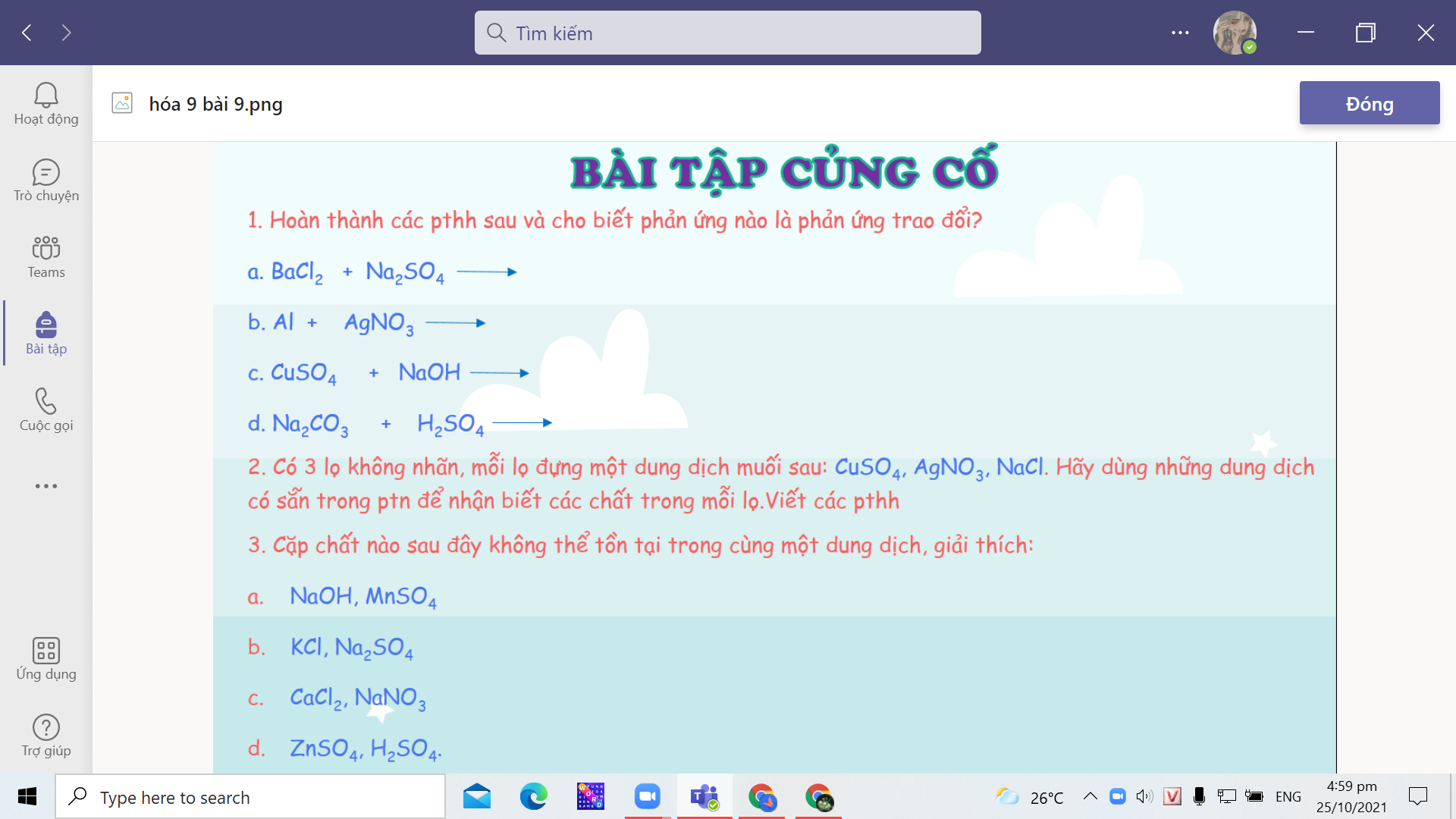
1.
a. \(BaCl_2+Na_2SO_4--->BaSO_4\downarrow+2NaCl\)
b. \(Al+3AgNO_3--->Al\left(NO_3\right)_3+3Ag\downarrow\)
c. \(CuSO_4+2NaOH--->Cu\left(OH\right)_2\downarrow+Na_2SO_4\)
d. \(Na_2CO_3+H_2SO_4--->Na_2SO_4+H_2O+CO_2\uparrow\)
Phản ứng trao đổi là PT: a, c, d
mình cần bài 2 hoặc 3, bài 1 làm rồi