Cho hình bình hành ABCD, có BD = x+2y+11=0
H(-1;-1) là trực tâm ABD
G(1;-9) là trọng tâm BCD
Tìm tọa độ ABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2023
Bài 3:
a: Ta có: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
Hình thang BDEC có \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
b: Để BD=DE=EC thì BD=DE và DE=EC
BD=DE thì ΔDBE cân tại D
=>\(\widehat{DBE}=\widehat{DEB}\)
mà \(\widehat{DEB}=\widehat{EBC}\)(hai góc so le trong, DE//BC)
nên \(\widehat{DBE}=\widehat{EBC}\)
=>\(\widehat{ABE}=\widehat{EBC}\)
=>BE là phân giác của góc ABC
=>E là chân đường phân giác kẻ từ B xuống AC
Xét ΔEDC có ED=EC
nên ΔEDC cân tại E
=>\(\widehat{EDC}=\widehat{ECD}\)
mà \(\widehat{EDC}=\widehat{DCB}\)(hai góc so le trong, DE//BC)
nên \(\widehat{ECD}=\widehat{DCB}\)
=>\(\widehat{ACD}=\widehat{BCD}\)
=>CD là phân giác của góc ACB
=>D là chân đường phân giác từ C kẻ xuống AB
Bài 2:
a: Ta có: ABCD là hình bình hành
=>AB//CD và AB=CD(1)
Ta có: M là trung điểm của AB
=>\(AM=MB=\dfrac{AB}{2}\left(2\right)\)
Ta có: N là trung điểm của CD
=>\(NC=ND=\dfrac{CD}{2}\left(3\right)\)
Từ (1),(2),(3) suy ra AM=MB=NC=ND
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b: Ta có AMCN là hình bình hành
=>AN//CM
Xét ΔDFC có
N là trung điểm của DC
NE//FC
Do đó: E là trung điểm của DF
=>DE=EF(4)
Xét ΔABE có
M là trung điểm của BA
MF//AE
Do đó: F là trung điểm của BE
=>BF=FE(5)
Từ (4) và (5) suy ra BF=FE=ED
24 tháng 4 2019
2.tự vẽ hình
a)Gọi O là giao điểm của hai đường chéo=>OD=OB(t/c)
Xét tgv OFD và tgv OEB có:
\(\widehat{FOD}=\widehat{EOB}\left(\text{đ}\text{ối}\text{đ}\text{ỉnh}\right)\)
\(DO=BO\left(cmt\right)\)
=> tgv OFD = tgv OEB (cgv-gn)
=> DF=BE
Mà DF//BE ( cùng vg với AC)
=> tg DEBF là hbn ( có cặp cạnh đối // và bằng nhau)
b) Ta có : \(\widehat{ADC}=\widehat{ABC}\)(hai góc so le trong)
\(\Rightarrow\widehat{CDK}=\widehat{CBH}\)
Xét tg CKD và tg CHB có :
\(\widehat{CDK}=\widehat{CBH}\)
\(\widehat{DKC}=\widehat{BHC}\left(=90\text{đ}\text{ộ}\right)\)
=> tg CKD = tg CHB (g.g)
\(\Rightarrow\frac{CK}{CD}=\frac{CH}{CB}\Rightarrow CD\cdot CH=CK\cdot CB\)
24 tháng 4 2019
c) Xét tg ABE và tg AHC có :
\(\widehat{AEB}=\widehat{AHC}\)
\(\widehat{A}:chung\)
=> tg ABE đồng dạng tg AHC (g.g)
\(\Rightarrow\frac{AB}{AC}=\frac{AE}{AH}\Rightarrow AB\cdot AH=AC\cdot AE\)(1)
Xét tg ADF và tg ACK có :
\(\widehat{A}:chung\)
\(\widehat{\text{AF}D}=\widehat{AKC}\)
=> tg ADF đồng dạng tg ACK
\(\Rightarrow\frac{AD}{AC}=\frac{\text{AF}}{AK}\Rightarrow AD\cdot AK=AC\cdot\text{AF}\)(2)
Xét tgv AFD và tgv CEB có :
AD=BC(gt)
DF=BE(cmt)
=> tg AFD=tg CEB (ch-cgv)
=> AF=CE (3)
Từ (1); (2); (3) ta có :
\(AB\cdot AH+AD\cdot AK=AC\left(AE+\text{AF}\right)=AC\left(AE\cdot CE\right)=AC^2\)
20 tháng 12 2022
Câu 10:
góc A=180-130=50 độ
góc B=(180+50)/2=230/2=115 độ
góc C=180-115=65 độ
CM
21 tháng 8 2019
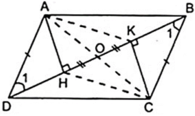
Từ giả thiết ta có:
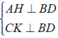
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
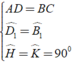
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
CM
9 tháng 12 2018
Ta chứng minh AH//CK, AH = CK (DAHD = DCKB) Þ AHCK là hình bình hành (cặp cạnh đối song song và bằng nhau)
