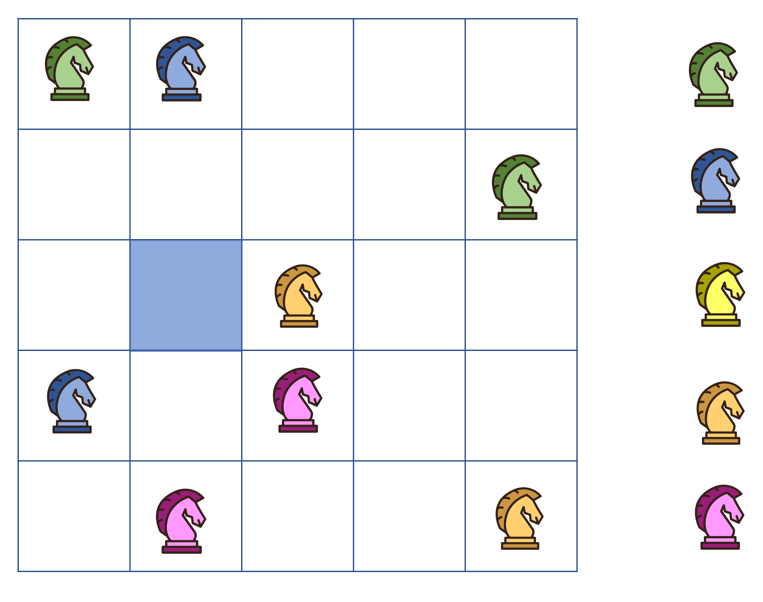
Cho một bàn cờ như hình vẽ. 25 quân cờ khác màu (5 màu) được xếp vào các ô sao cho mỗi màu chỉ xuất hiện 1 lần trong mỗi hàng, mỗi cột. Tìm màu của quân cờ trong ô được in đậm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
23 tháng 8 2021
| 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 |
| 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 |
| -1 | |||||||||
| 1 | |||||||||
| -1 | |||||||||
| 1 | |||||||||
| -1 | |||||||||
| 1 | |||||||||
| -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 | -1 | 1 |
Đánh số các ô bằng các số \(1\)và \(-1\)sao cho hai ô liền nhau cùng hàng hoặc cùng cột là khác nhau
(hình minh họa)
Khi đó tổng các ô trên bàn cờ là \(0\).
Khi xóa đi hai ô liền nhau cùng hàng hoặc cùng cột thì tổng đó không đổi (do xóa đi \(1\)và \(-1\)).
Giả sử có thể sau \(49\)lần xóa còn \(2\)ô góc đối diện.
Khi đó tổng hai ô còn lại đó là \(-1+\left(-1\right)=-2\)hoặc \(1+1=2\)(mâu thuẫn)
Do đó không thể có cách tô thỏa mãn.
2 tháng 8 2021
????????????????????????????????????????????????????????
CM
19 tháng 12 2019
Chọn A
Mỗi lần di chuyển, quân cờ chỉ có thể di chuyển một trong bốn cách sau: lên trên 1 ô (U), xuống dưới 1 ô (D), sang phải 1 ô (R), sang trái 1 ô (L). Quân cờ di chuyển bốn lần sẽ có 4 4 = 256 cách.
⇒ n ( Ω ) = 256 cách
Gọi A là biến cố quân cờ không trở về đúng vị trí ban đầu sau bốn lần di chuyển.
=> A ¯ là biến cố quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển.
Để quân cờ trở về đúng vị trí ban đầu sau bốn lần đi chuyển thì phải thực hiện 1 trong 3 trường hợp sau:
Trường hợp 1: Có một U, một D, một R, một L.
Xếp cách thực hiện U, D, R, L theo thứ tự có 4! = 24 cách.
Trường hợp 2: Có hai U, hai D.
Xếp cách thực hiện hai U, hai D theo thứ tự có 
cách.
Trường hợp 3: Có hai R, hai L.
Xếp cách thực hiện hai R, hai L theo thứ tự có 
cách.
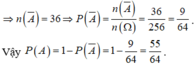
sai đề rồi bạm ê