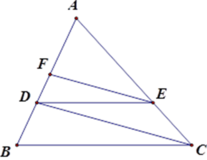
Cho tam giác ABC có AB = 9 ,cm, điểm D thuộc cạnh AB sao cho AD = 6 ,cm. Kẻ DE song song với BC ( (E thuộc AC) ), kẻ EF song song với CD ( (F thuộc AB) ). Tính độ dài AF .
GIÚP MÌNH VỚI CÀNG NHANH CÀNG TỐT, MÌNH SẼ TICK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 12 2019
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
Đáp án đúng là: A
Áp dụng định lí Thalès:
• Với DE // BC (E ∈ AC) ta có: \(\dfrac{{A{\rm{D}}}}{{AB}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{6}{{9}} = \dfrac{2}{3}\)
• Với EF // CD (F ∈ AB) ta có: \(\dfrac{{AF}}{{A{\rm{D}}}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{2}{3}\)
Suy ra: \({\rm{AF}} = \dfrac{2}{3}A{\rm{D}} = \dfrac{2}{3}.6 = 4(cm)\)
Vậy AF = 4 cm.
20 tháng 12 2015
434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!
5 tháng 11 2021
a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật
24 tháng 1 2019
ta có: DE// AC; D thuộc BC; E thuộc AB của tg ABC
=> AE/AB = CD/BC ( định lí Ta-lét) (*)
ta có: DF// AB ....
=> AF/AC = BD/BC ( định lí Ta-lét)
Từ (*) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{CD}{BC}+\frac{BD}{BC}=\frac{CD+BD}{BC}=\frac{BC}{BC}=1\)
hình tự vẽ
6 tháng 12 2023
Xét ΔCAB và ΔCED có
\(\widehat{CAB}=\widehat{CED}\)(hai góc so le trong, DE//AB)
\(\widehat{ACB}=\widehat{ECD}\)(hai góc đối đỉnh)
Do đó: ΔCAB đồng dạng với ΔCED
=>\(\dfrac{CA}{CE}=\dfrac{AB}{ED}=\dfrac{CB}{CD}\)
=>\(\dfrac{12}{CE}=\dfrac{18}{ED}=\dfrac{9}{3}=3\)
=>\(CE=\dfrac{12}{3}=4\left(cm\right);ED=\dfrac{18}{3}=6\left(cm\right)\)
Áp dụng định lí Ta-lét:
+với EF//CD ta có \(\frac{AF}{AD}=\frac{AE}{AC}\)
+với DE//BC tác có \(\frac{AE}{AC}=\frac{AD}{AB}\)
suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\),
tức là \(\frac{AF}{6}\)\(=\frac{6}{9}\)
=> AF=\(\frac{6.6}{9}=4\left(cm\right)\)
CHÚC BẠN HỌC TỐT