tìm giá trị của tham số m để biểu thức f(x)= ( -x^2 + 4(m+1)x + 1 - 4m^2 )/ -4x^2 +5x -2 luôn dương
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2: \(-4x^2+5x-2\)
\(=-4\left(x^2-\dfrac{5}{4}x+\dfrac{1}{2}\right)\)
\(=-4\left(x^2-2\cdot x\cdot\dfrac{5}{8}+\dfrac{25}{64}+\dfrac{7}{64}\right)\)
\(=-4\left(x-\dfrac{5}{8}\right)^2-\dfrac{7}{16}< =-\dfrac{7}{16}< 0\forall x\)
Sửa đề:\(f\left(x\right)=\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}\)
Để f(x)>0 với mọi x thì \(\dfrac{-x^2+4\left(m+1\right)x+1-4m^2}{-4x^2+5x-2}>0\forall x\)
=>\(-x^2+4\left(m+1\right)x+1-4m^2< 0\forall x\)(1)
\(\text{Δ}=\left[\left(4m+4\right)\right]^2-4\cdot\left(-1\right)\left(1-4m^2\right)\)
\(=16m^2+32m+16+4\left(1-4m^2\right)\)
\(=32m+20\)
Để BĐT(1) luôn đúng với mọi x thì \(\left\{{}\begin{matrix}\text{Δ}< 0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}32m+20< 0\\-1< 0\left(đúng\right)\end{matrix}\right.\)
=>32m+20<0
=>32m<-20
=>\(m< -\dfrac{5}{8}\)

Chọn A
Tam thức : -4x2+ 5x-1 có a= -4 và ∆ = -7< 0
suy ra -4x2+ 5x-1<0 với mọi x
Do đó h(x) luôn dương khi và chỉ khi
f(x) = -x2+ 4( m+1) x+ 1- 4m2 luôn âm
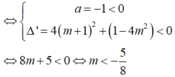
Vậy với m< -5/8 thì biểu thức h(x) luôn dương.

Chọn A.
Tam thức -4 x 2 + 5x - 2 có a = -4 <0, Δ = -7 < 0 suy ra -4 x 2 + 5x - 2 < 0, ∀x
Do đó 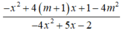
luôn dương khi và chỉ khi - x 2 + 4(m + 1)x + 1 - 4 m 2 luôn âm
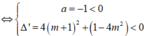

Vậy với 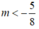 thì biểu thức
thì biểu thức 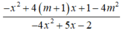 luôn dương.
luôn dương.

1.
Nếu \(m=0\), \(f\left(x\right)=2x\)
\(\Rightarrow m=0\) không thỏa mãn
Nếu \(x\ne0\)
Yêu cầu bài toán thỏa mãn khi \(\left\{{}\begin{matrix}m< 0\\\Delta'=\left(m-1\right)^2-4m^2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\left[{}\begin{matrix}m>1\\m< -\dfrac{1}{3}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow m< -\dfrac{1}{3}\)

`#3107.\text {DN}`
a)
\((2x-3)^2-x(3-x)+5x-4x^2+17\)
`= 4x^2 - 12x + 9 - 3x + x^2 + 5x - 4x^2 + 17`
`= x^2 - 10x + 26`
b)
`M = x^2 - 10x + 26`
`= [(x)^2 - 2*x*5 + 5^2] + 1`
`= (x - 5)^2 + 1`
Vì `(x - 5)^2 \ge 0` `AA` `x => (x - 5)^2 + 1 \ge 1` `AA` `x`
Vậy, giá trị biểu thức M luôn có giá trị dương với mọi x.