Tìm các phân số bằng nhau trong các phân số sau đây :
\(\frac{3}{7}\)\(\frac{9}{5}\)\(\frac{7}{8}\)\(\frac{51}{119}\)\(\frac{84}{96}\)\(\frac{189}{105}\)
Nhớ có cách giải chi tiết !!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phân số lớn nhất :\(\frac{9}{10}\)
Phân số bé nhất :\(\frac{1}{2}\)

Phân số bằng nhau là
* \(\frac{25}{35}=\frac{5}{7}\) Và \(\frac{55}{77}=\frac{5}{7}\)
\(\Rightarrow\frac{25}{35}=\frac{55}{77}\)
Các câu khác tương tự bạn nhé(Nhớ tích cho mk nha)

$\frac{2}{3} = \frac{{2 \times 3}}{{3 \times 3}} = \frac{6}{9}$
$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$
Vậy $\frac{2}{3} = \frac{6}{9}$ ; $\frac{3}{4} = \frac{9}{{12}}$
\(\dfrac{2}{3}=\dfrac{6}{9}\)
\(\dfrac{3}{4}=\dfrac{9}{12}\)

\(\frac{1}{5}=\frac{1.3}{5.3}=\frac{3}{15}\)
\(\frac{-10}{55}=\frac{-10\div5}{55\div5}=\frac{-2}{11}\)
Vậy ba cặp số phân số bằng nhau sau khi sử dụng tính chất cơ bản
2 .
\(\frac{-12}{-3}=\frac{-12:3}{-3:3}=\frac{-4}{-1};\frac{7}{-35}=\frac{7:7}{-35:7}=\frac{1}{-5};\frac{-9}{27}=\frac{-9:9}{27:9}=\frac{-1}{3}\)
3 .
\(15min=\frac{1}{4}\)giờ
\(90min=\frac{3}{2}\)giờ

Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 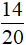
Ta rút gọn các phân số về dạng tối giản:
Do vậy ta có:
Phân số 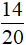

1/ ĐÁP ÁN:
\(\frac{-9}{33}=\frac{3}{-11}\); \(\frac{15}{9}=\frac{5}{3}\); \(\frac{-12}{19}=\frac{60}{-95}\)
2/ ĐÁP ÁN:
\(\frac{-7}{20}=\frac{3}{-18}=\frac{-9}{54}\ne\frac{12}{18}=\frac{-10}{-15}\ne\frac{14}{20}\)
3/ ĐÁP ÁN:
\(\frac{2}{3}=\frac{40}{60}\); \(\frac{3}{4}=\frac{45}{60}\); \(\frac{4}{5}=\frac{48}{60}\); \(\frac{5}{6}=\frac{50}{60}\)

ta có 2/7<5/7
1/3<3/5
Mà 2/7<1/3
Nên 2/7 là phân số có giá trị nhỏ nhất
K mik nha
Ta thấy :
\(\frac{2}{7}< \frac{5}{7}\)
\(\frac{1}{3}< \frac{3}{5}\left(\frac{5}{15}< \frac{9}{15}\right)\)
Mà \(\frac{2}{7}< \frac{1}{3}\left(\frac{2}{7}< \frac{2}{6}=\frac{1}{3}\right)\)
Vậy phân số bé nhất là \(\frac{2}{7}\)
Giả sử a > = b ko làm mất đi tính tổng quát của bài toán.
=> a= m+b (m>=0)
Ta có: \(\frac{a}{b}+\frac{b}{a}\)= \(\frac{b+m}{b}\)+ \(\frac{b}{b+m}\)=1 + \(\frac{m}{b}\)+\(\frac{b}{b+m}\)< 1 + \(\frac{m}{b+m}\)+\(\frac{b}{b+m}\)= 1 + \(\frac{m+b}{b+m}\)= 1+1=2
Vậy a/b + b/a < 2 (ĐPCM)