Bài 1 : Cho tam giác ABC nhọn . Các đường cao BE và CF cắt nhau tại H
a) Chứng minh : Tức giác AEHF nội tiếp đường tròn
b) Chứng minh : Tứ giác BFEC nội tiếp đường tròn
c) Chứng minh : Tam giác AEF đồng dạng với tam giác ABC
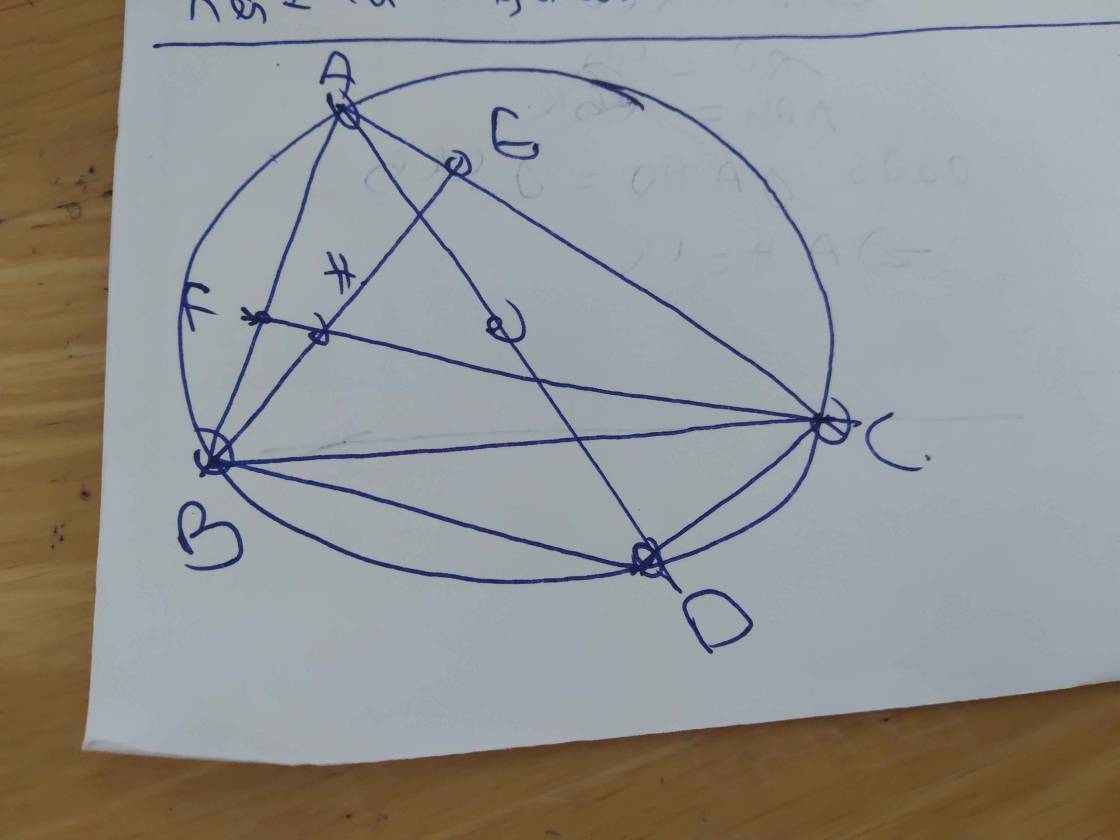
Bài 2 : Cho đường tròn (O) có đường kính AB và điểm C thuộc đường tròn đó (C khác A , B ).
Lấy điểm D thuộc dây BC (D khác B, C). Tia AD cắt cung nhỏ BC tại điểm E, tia AC cắt tia BE
tại điểm F.
1) Chứng minh rằng FCDE là tứ giác nội tiếp đường tròn.
2) Chứng minh rằng DA.DE = DB.DC.
3) Gọi I là tâm đường tròn ngoại tiếp tứ giác FCDE, chứng minh rằng IC là tiếp tuyến của
đường tròn (O)
Bài 3 : Cho nửa đường tròn tâm O đường kính AB. Lấy điểm C thuộc nửa đường tròn và điểm
D nằm trên đoạn OA. Vẽ các tiếp tuyến Ax, By của nửa đường tròn. Đường thẳng qua C, vuông
góc với CD cắt cắt tiếp tuyên Ax, By lần lượt tại M và N.
1) Chứng minh các tứ giác ADCM và BDCN nội tiếp được đường tròn.
2) Chứng minh rằng : \(\widehat{MDN}\) ̂ = 90o
3) Gọi P là giao điểm của AC và DM, Q là giao điểm của BC và DN. Chứng minh rằng PQ
song song với AB.