Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) x2 - 2x - 3 = 0
Dễ thấy pt có a - b + c = 0 nên có hai nghiệm x1 = -1 ; x2 = 3
Vậy phương trình có hai nghiệm x1 = -1 ; x2 = 3
b) -x2 + 7x - 6 = 0
Dễ thấy pt có a + b + c = 0 nên có hai nghiệm x1 = 1 ; x2 = 6
Vậy phương trình có hai nghiệm x1 = 1 ; x2 = 6
*đths e chưa làm đc vì mới lớp 8 :v*
Hàm số đồng biến trên \(\left(-\infty;1\right)\) do \(a=-1< 0\) và \(-\dfrac{b}{2a}=1\)
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)
TXĐ: D = [0; 2]
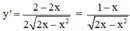
+ Hàm số đồng biến
⇔ y’ > 0
⇔ 0 < x < 1.
+ Hàm số nghịch biến
⇔ y’ < 0
⇔ 1 < x < 2.
Vậy hàm số đồng biến trên khoảng (0; 1), nghịch biến trên khoảng (1; 2).
Đáp án B
* Hàm số bậc nhất y = ax + b đồng biến khi a > 0 và hàm số này nghịch biến khi a < 0 .
Do đó, hàm số y = 3x đồng biến trên R nên cũng đồng biến khi x < 0 .
Hàm số y = -4x nghịch biến trên R.
* Xét hàm số y = ax2 (a ≠ 0)
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Trong hai hàm số y = 3x2 và y = -4x2 chỉ có hàm số y = -4x2 đồng biến khi x < 0
Vậy trong các hàm số đã cho chỉ có hàm số y = 3x và y = -4x2 đồng biến x < 0.
Cho hàm số: y = -3 x 2 . Ta có: a = -3 < 0 nên hàm số đồng biến khi x < 0.
Chọn C) Khi -15 < x < 0, hàm số đồng biến.
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Câu 94: B
Câu 95: \(A=\left(-\dfrac{b}{2a};-\dfrac{b^2-4ac}{4a}\right)\)
\(\Leftrightarrow A\left(\dfrac{-2}{2\cdot\left(-1\right)};\dfrac{-\left(2^2-4\cdot\left(-1\right)\cdot3\right)}{4\cdot\left(-1\right)}\right)\)
\(\Leftrightarrow A\left(1;4\right)\)
Câu 96 là câu nào v ạ.