Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
bài 1
a) \(-\frac{1}{3}xy\).(3\(x^2yz^2\))
=\(\left(-\frac{1}{3}.3\right)\).\(\left(x.x^2\right)\).(y.y).\(z^2\)
=\(-x^3\).\(y^2z^2\)
b)-54\(y^2\).b.x
=(-54.b).\(y^2x\)
=-54b\(y^2x\)
c) -2.\(x^2y.\left(\frac{1}{2}\right)^2.x.\left(y^2.x\right)^3\)
=\(-2x^2y.\frac{1}{4}.x.y^6.x^3\)
=\(\left(-2.\frac{1}{4}\right).\left(x^2.x.x^3\right).\left(y.y^2\right)\)
=\(\frac{-1}{2}x^6y^3\)
Bài 3:
a) \(f\left(x\right)=-15x^2+5x^4-4x^2+8x^2-9x^3-x^4+15-7x^3\)
\(f\left(x\right)=\left(5x^4-x^4\right)-\left(9x^3+7x^3\right)-\left(15x^2+4x^2-8x^2\right)+15\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
b)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=4\cdot1^4-16\cdot1^3-11\cdot1^2+15\)
\(f\left(1\right)=-8\)
\(f\left(x\right)=4x^4-16x^3-11x^2+15\)
\(f\left(-1\right)=4\cdot\left(-1\right)^4-16\cdot\left(-1\right)^3-11\cdot\left(-1\right)^2+15\)
\(f\left(-1\right)=24\)
a) \(\left(x+5\right)^2-\left(x-5\right)^2-20x+2\)
\(=x^2+10x+25-x^2+10x-25-20x+2\)
\(=2\) không phụ thuộc vào \(x\)
b) \(\left(x+3\right)\left(x-5\right)-\left(x-1\right)^2\)
\(=x^2-2x-15-x^2+2x-1\)
\(=-16\) không phụ thuộc vào \(x\)
c) \(\left(3x+2\right)\left(x-2\right)-x\left(3x-5\right)+8\)
\(=3x^2-4x-4-3x^2+5x+8\)
\(=x+8\) câu này đề sai.
d) \(2.\left(3x+1\right)\left(2x+5\right)-6x.\left(2x+4\right)-10\left(x-1\right)\)
\(=2.\left(6x^2+17x+5\right)-\left(12x^2+24x\right)-10x+10\)
\(=12x^2+34x+10-12x^2-24x-10x+10\)
\(=20\) không phụ thuộc vào \(x\)
a) ( x + 5 )2 - ( x - 5 )2 - 20x + 2
= x2 + 10x + 25 - ( x2 - 10x + 25 ) - 20x + 2
= x2 + 10x + 25 - x2 + 10x - 25 - 20x + 2
= 2 ( đpcm )
b) ( x + 3 )( x - 5 ) - ( x - 1 )2
= x2 - 2x - 15 - ( x2 - 2x + 1 )
= x2 - 2x - 15 - x2 + 2x - 1
= -16 ( đpcm )
c) ( 3x + 2 )( x - 2 ) - x( 3x - 5 ) + 8
= 3x2 - 4x - 4 - 3x2 + 5x + 8
= x + 4 ( lỗi đề )
d) 2( 3x + 1 )( 2x + 5 ) - 6x( 2x + 4 ) - 10( x - 1 )
= 2( 6x2 + 17x + 5 ) - 12x2 - 24x - 10x + 10
= 12x2 + 34x + 10 - 12x2 - 24x - 10x + 10
= 20 ( đpcm )
a, \(f\left(x\right)=2x^2\left(x-1\right)-5\left(x+2\right)-2x\left(x-2\right)\)
\(=2x^3-2x^2-5x-10-2x^2+4x=2x^3-4x^2-x-10\)
b, \(g\left(x\right)=x^2\left(2x-3\right)-x\left(x+1\right)-\left(3x-2\right)\)
\(=2x^3-3x^2-x^2-x-3x+2=2x^3+2-4x^2-4x\)
b, Ta có : \(H\left(x\right)=F\left(x\right)-G\left(x\right)=2x^3-4x^2-x-10-2x^3+4x^2+4x-2\)
\(\Leftrightarrow3x-12=0\Leftrightarrow x=4\)
a) \(5x^2-2x\left(3x+\frac{3}{2}\right)=-x^2-3x=-x\left(x+3\right)=-3\left(3+3\right)=-18\)
b) \(3x\left(x-4y\right)-\frac{12}{5}y\left(y-5x\right)=3x^2-\frac{12}{5}y^2=3\left(x^2-\frac{4}{5}y^2\right)\)
\(=3\left(4^2-\frac{4}{5}.5^2\right)=3.\left(-4\right)=-12\)
c) \(\left(x-2\right)^2-\left(x+7\right)\left(x-7\right)=x^2-4x+4-x^2+49=-4x+53=-4.3+53=41\)
d) \(x^2+12x+36=\left(x+6\right)^2=\left(64+6\right)^2=70^2=4900\)
e) \(\left(x-3\right)^2-\left(x-4\right)\left(x+4\right)=x^2-6x+9-x^2+16=-6x+25=-6\left(-1\right)+25\)
= 31
f) \(\left(3x+2y\right)^2-4y\left(3x+y\right)=9x^2+12xy+4y^2-12xy-4y^2=9x^2=9\left(-\frac{1}{3}\right)^2=1\)
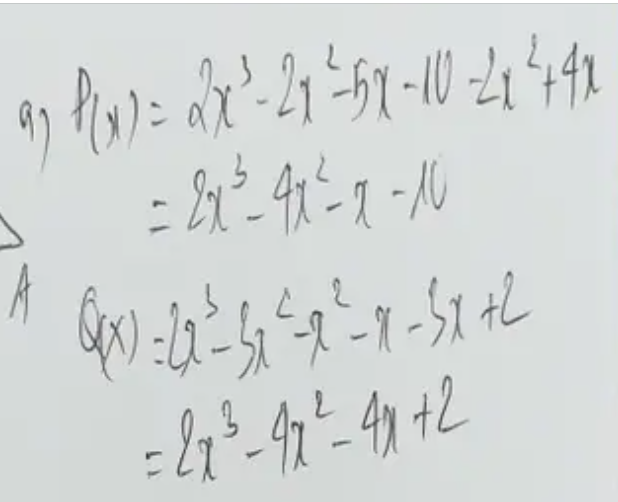
Bài 1:
Mình sửa lại đề 1 chút: \(x+x^3+x^5+...+x^{101}=P\left(x\right)\)
Số hạng trong dãy là: (101-1):2+1=51
P(-1)=(-1)+(-1)3+(-1)5+...+(-1)101
Vì (-1)2n+1=-1 với n thuộc Z
=> P(-1)=(-1)+(-1)+....+(-1) (có 51 số -1)
=> P(-1)=-51