giải phương trình
10x^2-11x-6=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Xét tam thức \(f\left( x \right) = 7{x^2} - 19x - 6\) có \(\Delta = 529 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{2}{7},{x_2} = 3\) và có \(a = 7 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là đoạn \(\left[ { - \frac{2}{7};3} \right]\)
b) \( - 6{x^2} + 11x > 10 \Leftrightarrow - 6{x^2} + 11x - 10 > 0\)
Xét tam thức \(f\left( x \right) = - 6{x^2} + 11x - 10\) có \(\Delta = - 119 < 0\)và có \(a = - 6 < 0\)
Ta có bảng xét dấu như sau
Vậy bất phương trình vô nghiệm
c) \(3{x^2} - 4x + 7 > {x^2} + 2x + 1 \Leftrightarrow 2{x^2} - 6x + 6 > 0\)
Xét tam thức \(f\left( x \right) = 2{x^2} - 6x + 6\) có \(\Delta = - 12 < 0\)và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
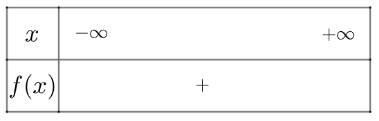
Vậy bất phương trình có vô số nghiệm
d) Xét tam thức \(f\left( x \right) = {x^2} - 10x + 25\) có \(\Delta = 0\), có nghiệm kép \({x_1} = {x_2} = 5\) và có \(a = 1 > 0\)
Ta có bảng xét dấu như sau
Vậy nghiệm của bất phương trình là \(x = 5\)
DH
1
14 tháng 6 2017
\(10x^2+11x+3\ge0\)
\(\Leftrightarrow10x^2+5x+6x+3\ge0\)
\(\Leftrightarrow5x\left(2x+1\right)+3\left(2x+1\right)\ge0\)
\(\Leftrightarrow\left(5x+3\right)\left(2x+1\right)\ge0\)
\(\Rightarrow x\le-\frac{3}{5};-\frac{1}{2}\le x\)
26 tháng 10 2015
bạn phải phân tích đa thức thành nhân tử để hạ bậc. Một mẹo mình mách bạn thế này . bạn tìm một giá trị của x thỏa mãn thì dựa vào đó đó phân tich. Thông thường giá trị đó là ước của hằng số trong vế trái ví dụ câu a bạn thay ước của 12. mình thấy -1 thỏa mãn vậy khi phân tích đa thức thành nhân tử chắc chắn sẽ xuất hiện nhân tử là x+1 và dựa vào đó mình phân tích như sau:
x3-6x2+5x+12=0
<=> x3+x2-7x2-7x+12x+12=0
<=> (x3+x2)-(7x2+7x)+(12x+12)=0
<=> x2(x+1)-7x(x+1)+12(x+1)=0
<=> (x+1)(x2-7x+12)=0
Phân tích tiếp nhóm x2-7x+12 = x2-3x-4x+12 = x(x-3)-4(x-3) = (x-3)(x-4)
vậy phương trình tương đương
<=> (x+1)(x-3)(x-4) = 0
đến đây dễ dàng suy ra x = -1; 3; 4
Các câu còn lại tương tự bạn tự làm vì quá nhiều mình không gõ được
DN
2
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 2 2020
\(2x^3+3x^2-32x-48=0\)
\(\Leftrightarrow2x^3-32x+3x^2-48=0\)
\(\Leftrightarrow2x\left(x^2-16\right)+3\left(x^2-16\right)=0\)
\(\Leftrightarrow\left(2x+3\right)\left(x^2-16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\pm4\\x=-\frac{3}{2}\end{matrix}\right.\)
b/ \(\Leftrightarrow10x^2-15x+4x-6=0\)
\(\Leftrightarrow5x\left(2x^2-3\right)+2\left(2x-3\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(5x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=\frac{3}{2}\\x=-\frac{2}{5}\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
13 tháng 2 2020
Lời giải:
a)
$10x^2-11x-6=0$
$\Leftrightarrow 10x^2-15x+4x-6=0$
$\Leftrightarrow 5x(2x-3)+2(2x-3)=0$
$\Leftrightarrow (2x-3)(5x+2)=0$
$\Rightarrow 2x-3=0$ hoặc $5x+2=0$
$\Rightarrow x=\frac{3}{2}$ hoặc $x=-\frac{2}{5}$
b)
$2x^3+3x^2-32x=48$
$\Leftrightarrow 2x^3+3x^2-32x-48=0$
$\Leftrightarrow 2x^3-8x^2+11x-44x+12x-48=0$
$\Leftrightarrow 2x^2(x-4)+11x(x-4)+12(x-4)=0$
$\Leftrightarrow (x-4)(2x^2+11x+12)=0$
$\Leftrightarrow (x-4)[2x(x+4)+3(x+4)]=0$
$\Leftrightarrow (x-4)(x+4)(2x+3)=0$
$\Rightarrow x-4=0; x+4=0$ hoặc $2x+3=0$
$\Rightarrow x=\pm 4$ hoặc $x=\frac{-3}{2}$
TN
1
4 tháng 4 2020
a) x^4 - 5x^2 + 4 = 0
<=> (x^2 - 1)(x^2 - 4) = 0
<=> x^2 - 1 = 0 hoặc x^2 - 4 = 0
<=> x = +-1 hoặc x = +-2
b) x^4 - 10x^2 + 9 = 0
<=> (x^2 - 1)(x^2 - 9) = 0
<=> x^2 - 1 = 0 hoặc x^2 - 9 = 0
<=> x = +-1 hoặc x = +-3
c) x^3 + 6x^2 + 11x + 6 = 0
<=> (x^2 + 5x + 6)(x + 1) = 0
<=> (x + 2)(x + 3)(x + 1) = 0
<=> x + 2 = 0 hoặc x + 3 = 0 hoặc x + 1 = 0
<=> x = -2 hoặc x = -3 hoặc x = -1
d) x^3 + 9x^2 + 26x + 24 = 0
<=> (x^2 + 7x + 12)(x + 2) = 0
<=> (x + 3)(x + 4)(x + 2) = 0
<=> x + 3 = 0 hoặc x + 4 = 0 hoặc x + 2 = 0
<=> x = -3 hoặc x = -4 hoặc x = -2
YT
15 tháng 6 2018
\(4x^4-11x^2+6=0\)
\(\Leftrightarrow4x^4-8x^2-3x^2+6=0\)
\(\Leftrightarrow4x^2\left(x^2-2\right)-3\left(x^2-2\right)=0\)
\(\Leftrightarrow\left(x^2-2\right)\left(4x^2-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-2=0\\4x^2-3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\pm\sqrt{2}\\x=\pm\sqrt{\frac{3}{4}}\end{cases}}\)
\(S=\left\{\pm\sqrt{2};\pm\sqrt{\frac{3}{4}}\right\}\)
nếu có sai bn thông cảm nha
DM
2
8 tháng 1 2017
ta có x3-6x2+11x-6=0
hay x3-x2-5x2-+5x+6x-6=0
=>x(x-1) - 5x(x-1)+6(x-1)=0
(x-1).(x-5x+6)=0 <=> (x-1)(x2-2x-3x+6)=0
(x-1)(x(x-2)-3(x-2)=0
(x-1)(x-2)(x-3)=0 <=> x-1=0 hoặc x-2=0 hoặc x-3=0
<=> x=1 hoặc x=2 hoặc x=3
vậy S ={1;2;3}
15 tháng 6 2018
Đặt \(a=x^2\)
\(\Rightarrow4a^2-11a+6=0\)
ta có: \(\Delta=11^2-4.4.6=121-96=25>0\)
=> Phương trình có 2 nghiệm phân biệt: \(a1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{11+\sqrt{25}}{2.4}=\frac{16}{8}=2\Leftrightarrow x^2=2\Leftrightarrow x=\pm\sqrt{2}\)
\(a2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{11-\sqrt{25}}{2.4}=\frac{6}{8}=\frac{3}{4}\)\(\Leftrightarrow x^2=\frac{3}{4}\Leftrightarrow x=\pm\sqrt{\frac{3}{4}}\)