Tam giác ABC có AB< AC. Gọi d là đường trung trực của BC. E là giao điểm của d với AC.
Gọi K là 1 điểm bất kì thuộc d (K khác E). So sánh chu vi tam giác AKB và AEB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 3 2018
Gọi I là giao điểm của đường trung trực của BC với BC . Nối KC
Ta có tam giác EIC = tam giác EIB ( c.g.c )
=> CE = BE ( hai cạnh tương ứng )
chu vi tam giác AEB = AE + AB + BE = AE + AB + CE ( do BE = CE )
=> chu vi tam giác ABE = AB + AC ( do AE + CE = AC )
tam giác KIB = tam giác KIC ( c.g.c )
=> KB = KC ( hai cạnh tương ứng )
chu vi tam giác AKB = AK + BK + AB = AK + KC + AB ( do BK = CK )
xét tam giác ACK theo bất đẳng thức tam giác ta có
AK + CK > AC
=> AK + CK + AB > AC + AB
=> chu vi tam giác ABK > chu vi tam giác ABE
20 tháng 4 2016
)Tam giác ABC có AB=30cm, AC=40cm. Trên tia đối của tia AC lấy điểm D sao cho AD=AB. Qua A kẻ đường d vuông góc với BD. Gọi M là điểm bất kì thuộc đường thẳng d. Tìm giá trị nhỏ nhất của tổng BM+MC
CM
21 tháng 11 2019
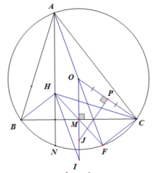
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)