Cho ΔABC cân ở A (∠A < 90o). Vẽ BH ⊥ AC (H ∈ AC), CK ⊥ AB (K ∈ AB).cm AI đi qua tđ M của BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2020
I là giao BH, CK phải ko bạn
Xét tgABC cân tại A có BI vg AC và CI vg AB
->I là trực tâm tg ABC
->AI vg bc
->Gọi AI cắt BC tại L
->AL là dg cao đồng thời là đường trung tuyến(t/c tg cân)
->dpcm
CM
10 tháng 9 2017
Xét ΔAIK vuông tại K và ΔAIH vuông tại H có:
AH = AK (theo phần a)
AI chung
⇒ ΔAIK = ΔAIH (cạnh huyền – cạnh góc vuông).
⇒ góc IAK = góc IAH (hai góc tương ứng)
Vậy AI là tia phân giác của góc A.
25 tháng 2 2022
a: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}\) chung
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
b: Xét ΔKCB vuông tại K và ΔHBC vuông tại H có
BC chung
KB=HC
Do đó: ΔKCB=ΔHBC
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
=>ΔBIC cân tại I
Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
Do đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
c: Ta có: ΔABC cân tại A
mà AI là đường phân giác
nên AI là đường cao
d: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
CM
24 tháng 11 2017
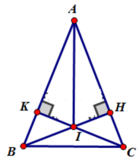
Xét ΔABH vuông tại H và ΔACK vuông tại K có:
AB = AC (Do ΔABC cân tại A)
góc A chung
Nên ΔABH = ΔACK (cạnh huyền – góc nhọn) ⇒ AH = AK (hai cạnh tương ứng).
23 tháng 4 2020
a) Sửa đề: AH = AK
Xét t/giác ABH và t/giác ACE
có: AB = AC (gt)
\(\widehat{AHB}=\widehat{AKC}=90^0\)(gt)
\(\widehat{A}\) : chung
=> t/giác ABH = t/giác ACK (Ch - gn)
=> AH = AK (2 cạnh t/ứng)
b) Ta có: \(\widehat{ABI}+\widehat{IBC}=180^0\)(kề bù)
\(\widehat{ACI}+\widehat{ICB}=180^0\)(kề bù)
Mà \(\widehat{ABI}=\widehat{ACI}\)(vì t/giác ABH = t/giác ACK)
=> \(\widehat{IBC}=\widehat{ICB}\) t/giác BIC cân tại I => IB = IC
Xét t/giác ABI và t/giác ACI
có: AB = AC (gt)
BI = IC (gt)
AI : chung
=> t/giác ABI = t/giác ACI (c.c.c)
=> \(\widehat{BAI}=\widehat{CAI}\)(2 góc t/ứng)
=> AI là tia p/giác cảu góc A
b) Gọi O là giao giểm của AI và BC
Xét t/giác ABO và t/giác ACO
có: AB = AC (gt)
AO: chung
\(\widehat{BAO}=\widehat{OAC}\)(cmt)
=> t/giác ABO = t/giác ACO (c.g.c)
=> \(\widehat{AOB}=\widehat{AOC}\)(2 góc t/ứng)
Mà \(\widehat{AOB}+\widehat{AOC}=180^0\)(kề bù)
=> \(\widehat{AOB}=\widehat{AOC}=90^0\)
=> AO \(\perp\)BC hay AO \(\perp\)BC
d) Ta cos: t/giác ABO = t/giác ACO (cmt)
=> BO = OC (2 cạnh t/ứng)
=> O là trung điểm của BC
DO A; I; O thẳng hàng => AI đi qua trung điểm của BC
1 tháng 3 2022
a: Xét ΔAMB và ΔAMC có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔAMB=ΔAMC
b: Xét ΔABH và ΔACK có
\(\widehat{BAH}\) chung
AB=AC
\(\widehat{ABH}=\widehat{ACK}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
M
1 tháng 3 2022
a, xét tam giác AMB và tam giác AMC có: AM chung
AB = AC do tam giác ABC cân tại A (gt)
góc BAM = góc CAM do AM là pg của góc BAC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
b, xét tam giác BKC và tam giác CHB có :BC chung
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc BKC = góc CHB = 90
=> tam giác BKC = tam giác CHB (ch-gn)
=> BH = CK (đn)
T
19 tháng 2 2020
a, xét tam giác AMB và tam giác AMC có: AM chung
AB = AC do tam giác ABC cân tại A (gt)
góc BAM = góc CAM do AM là pg của góc BAC (gt)
=> tam giác AMB = tam giác AMC (c-g-c)
b, xét tam giác BKC và tam giác CHB có :BC chung
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
góc BKC = góc CHB = 90
=> tam giác BKC = tam giác CHB (ch-gn)
=> BH = CK (đn)
oooooooooooooooooooooooooooooooooooooooooooookkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk