VẼ HỘ MK CÁI HÌNH VỚI !!!!!
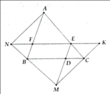
Cho tam giác ABC vuông tại A, M là điểm tùy ý trên đoạn AC (\(M\ne A;C\) ). Vẽ đường tròn tâm O đường kính MC cắt BC tại E. BM cắt ( O) tại N, AN cắt ( O) tại D. Lấy I đối xứng với M qua A. Lấy K đối xứng với M qua E. CM:
a) Tứ giác BANC nội tiếp
b) CA là phân giác góc BCD
c) Gỉa sử góc ABC =60* và \(AM=\frac{1}{3}.AC\). Tứ giác BMCK là hình gì?
d) Tìm vị trí điểm M để đường tròn ngoại tiếp tam giác BIK có bán kính nhỏ nhất


a) Vì MC là đường kính (O) mà \(N\in\left(O\right)\)
\(\Rightarrow\widehat{MNC}=90^o\).Lại có \(\widehat{BAC}=90^o\)
=> B,A,N,C cùng thuộc 1 đường tròn
=> Tứ giác BANC nội tiếp