Cho tam giác abc có ba góc nhọn đường tròn tâm O đường kính BC cắt AC tại E cắt AC tại F . Các tia BF và CE cắt nha tại H . CMR a) Gọi K là giao điểm của AH và BC. CMR: FB là phân giác góc EFK b) Gọi M là trung điểm BH. CMR: EMKF nội tiếp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 3 2018
a, Có : góc BEC = 90 độ ( góc nt chắn nửa đường tròn )
góc BFE = 90 độ ( góc nt chắn nửa đường tròn )
=> CE vuông góc với AB
BF vuông góc với AC
Mà BF cắt CE ở H
=> H là trực tâm tam giác ABC
=> AH vuông góc với BC
9 tháng 3 2018
b, Đề phải là cm FB là phân giác EFQ chứ bạn !
C/m được tứ giác CFHQ nt => góc CFQ = góc CHQ
Mà góc CHQ = góc CBE ( cùng phụ với góc EBC )
=> góc CFQ = góc CBE = góc AFE ( vì tứ giác BEFC nt )
Lại có : góc AFE + góc EFH = 90 độ và góc CEQ + góc HEQ = 90 dộ
=> góc EFH = góc KFQ
=> FB là phân giác góc EFQ
26 tháng 12 2021
a: Xét tứ giác AEHF có
\(\widehat{AEH}+\widehat{AFH}=180^0\)
Do đó: AEHF là tứ giác nội tiếp
11 tháng 5 2023
c: Theo câu b, ta được: H là tâm đường tròn ngoại tiếp ngũ giác DEKFO
OH vuông góc MN
=>MN là đường kính của (H)
=>HM=HN
6 tháng 1 2022
a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC
CM
17 tháng 2 2018
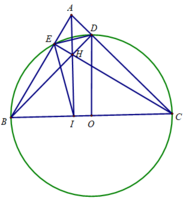
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)
