Bài 4: Cho một lò xo đàn hồi nằm ngang ở trạng thái ban đầu không bị biến dạng. Khi tác dụng một lực F = 3N kéo lò xo theo phương ngang ta thấy nó giãn được 2cm. Tính giá trị thế năng đàn hồi của lò xo.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải
+ Ta có độ biến dạng của lò xo so với vị
trí ban đầu: Δl=2cm=0,02m
Lực đàn hồi của lò xo khi đó: F d h = | k Δ l |
Ta suy ra độ cứng của lò xo: k = F d h Δ l = 3 0 , 02 = 150 N / m
=> Thế năng đàn hồi của lò xo tại vị trí đó: W t = 1 2 k Δ l 2 = 1 2 .150. 0 , 02 2 = 0 , 03 J
Đáp án: C

Độ cứng của lò xo:
\(k=\dfrac{F}{\Delta l}=\dfrac{3}{0,02}=150\)N/m
Thế năng đàn hồi:
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot150\cdot0,02^2=0,03J\)

a. Ta có lực đàn hồi
F = k . | Δ l | ⇒ k = F | Δ l | ⇒ k = 2 0 , 01 ⇒ k = 200 N / m W t d h = 1 2 k . ( Δ l ) 2 = 1 2 .100.0 , 01 2 = 5.10 − 3 ( J )
b. Theo độ biến thiên thế năng
A = 1 2 k . ( Δ l 1 ) 2 − 1 2 k . ( Δ l 2 ) 2 = 1 2 .100 ( 0 , 02 2 − 0 , 035 2 ) = - 0 , 04125 ( J )

Chọn A.
Ta có: F đ h = k . ∆ l ⇒ k = F đ h / ∆ l = 3/0,02 = 150 N/m.
Công do lực đàn hồi thực hiện khi lò xo được kéo dãn thêm từ 2 cm đến 4 cm có giá trị là:
A F đ h = 1 2 k ( ∆ l 1 ) 2 - 1 2 k ∆ l 2 2
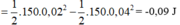

\(\Delta l=4cm=0,04m\)
a)Độ cứng lò xo:
\(k=\dfrac{F}{\Delta l}=\dfrac{10}{0,04}=250\)N/m
b)Thế năng đàn hồi của lò xo bị nén lại 6cm:
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot250\cdot0,06^2=0,45J\)
c)Độ biến thiên thế năng đàn hồi:
\(A=W_{đh1}-W_{đh2}=\dfrac{1}{2}kx'^2-0,45\)
\(=\dfrac{1}{2}\cdot250\cdot0,03^2-0,45=-0,3375J\)
Công này có tác dụng chống lại sự biến dạng.

\(\left|F\right|=kx\Rightarrow k=\dfrac{\left|F\right|}{x}=\dfrac{10}{0,05}=200N/m\)
\(A=\dfrac{1}{2}k\left(\Delta l\right)^2=\dfrac{1}{2}.200.0,05^2=0,25J\)
Đáp án: A

a) Độ lớn của lực đàn hồi:
![]()
b) Thế năng đàn hồi:
![]()
c) Công thực hiện của lò xo:
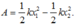
thay số:
![]()
Công A<0 vì lực đàn hồi ngược với chiều biến dạng, công của lực đàn hồi là công cản.

Chọn đáp án C
W d h = 1 2 k x 2 = 1 2 . 100 . 0 , 02 2 = 0 , 02 J
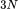 kéo lò xo theo phương ngang ta thấy nó dãn được
kéo lò xo theo phương ngang ta thấy nó dãn được 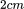 . Thế năng đàn hồi của lò xo có giá trị bằng
. Thế năng đàn hồi của lò xo có giá trị bằng
Gía trị thế năng đàn hồi của lò xo là :
\(W_{đh1}=\frac{kx_1^2}{2}=\frac{150\left(0,02\right)^2}{2}=0,03\left(J\right)\)