Question

[Kiều Thị Mai]

Bài 1 : Tam giác ABC có M là trung điểm BC, AM là tia phân giác của góc A. Kẻ MH vuông góc với AB, MK  vuông góc với AC. Chứng minh rằng :

a)      MH = MK

b)      Góc B bằng góc C

Bài 2 : Cho tam giác ABC cân tại A. Kẻ BD vuông với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm BD và CE. Chứng minh rằng :

1. Tam giác ADB bằng tam giác AEC
2. Tam giác ADK bằng tam giác AEK
3. AK là tia phân giác của góc A

Bài 3 : Cho tam giác ABC  cân ở A  ( góc A <  90 độ ). Vẽ BH  vuông góc với AC ( H thuộc AC), CK vuông góc với AB ( K thuộc AB )

      A . CMR : AH = AK

      B . Gọi I là giao điểm của BH và CK. CMR : AI là phân giác của góc A

      C . Gọi M là trung điểm của BC. CMR : AM vuông góc với BC

Bài 4 : Cho tam giác BFC cân tại B. Kẻ FE vuông góc với BC tại E, CA vuông góc với BF tại A.

a)      CMR: Tam giác BEF = tam giác BAC

b)     FE cắt CA tại D. CMR : BD là tia phân giác của góc ABC

c)      Gọi M là trung điểm của FC. CMR: BM vuông góc với AE

Answer 1

[Tran Le Khanh Linh]

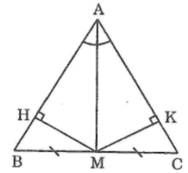
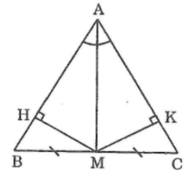
a)Xét tam giác HMA vuông tại H và tam giác KMA vuông tại K có:

AM là cạnh chung

MAH = MAK (AM là tia phân giác của A)

=> Tam giác HMA = Tam giác KMA (cạnh huyền - góc nhọn)

=> MH = MK (2 cạnh tương ứng)

Xét tam giác HBM vuông tại H và tam giác KCM vuông tại K có:

MH = MK

b) BM = CM (M là trung điểm của BC)

=> Tam giác HBM = Tam giác KCM (cạnh huyền - cạnh góc vuông)

=> \(\widehat{B}=\widehat{C}\)(2 góc tương ứng)

Nguồn: Phương An (h.vn)