Cho phương trình
\(x^2-\left(5m-1\right)x+6m^2-2m=0\)0
tính tổng và tích 2 nghiệm x1, x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 2 2020
a, \(\Delta=\left(5m-1\right)^2-4\left(6m^2-2m\right)=25m^2-10m+1-24m^2+8m\)
\(=m^2-2m+1=\left(m-1\right)^2\ge0\forall m\left(đpcm\right)\)
c, Theo hệ thức Vi-lét ta có: \(\hept{\begin{cases}x_1+x_2=5m-1\\x_1x_2=6m^2-2m\end{cases}}\)
\(\Rightarrow x^2_1+x^2_2=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)
\(\Leftrightarrow\left(5m-1\right)^2-2\left(6m^2-2m\right)=1\)
\(\Leftrightarrow25m^2-10m+1-12m^2+4m=1\)
\(\Leftrightarrow13m^2-6m=0\)
\(\Leftrightarrow m\left(13m-6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\13m-6=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\m=\frac{6}{13}\end{cases}}\)
Vậy \(\orbr{\begin{cases}m=0\\m=\frac{6}{13}\end{cases}}\) thì pt có 2 nghiệm \(x_1;x_2\) thỏa mãn \(x^2_1+x^2_2=1\)
CM
10 tháng 1 2019
Phương trình (2m - 1) x 2 - 2(m + 4)x + 5m + 2 = 0 ( m ≠ 1 2 )
8 tháng 4 2022
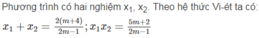
a: \(\text{Δ}=\left(5m-1\right)^2-4\left(6m^2-2m\right)\)
\(=25m^2-10m+1-24m^2+8m=m^2-2m+1=\left(m-1\right)^2>=0\)
Do đó: Phương trình luôn có nghiệm
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2=1\)
\(\Leftrightarrow\left(5m-1\right)^2-2\left(6m^2-2m\right)=1\)
\(\Leftrightarrow25m^2-10m+1-12m^2+4m-1=0\)
\(\Leftrightarrow13m^2-6m=0\)
=>m(13m-6)=0
=>m=0 hoặc m=6/13
24 tháng 4 2022
Cho phương trình: x^2 - 2(m-1)x + m-3=0 (m là tham số). Tìm m để phương trình có hai nghiệm phân biệt cùng dương
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
22 tháng 5 2021
Ta có: \(\Delta=4m^2+4m-11\)
Để phương trình có 2 nghiệm phân biệt \(\Leftrightarrow4m^2+4m-11>0\)
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m+3\\x_1x_2=2m+5\end{matrix}\right.\)
Để phương trình có 2 nghiệm dương phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}4m^2+4m-11>0\\2m+3>0\\2m+5>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< \dfrac{-1-2\sqrt{3}}{2}\\m>\dfrac{-1+2\sqrt{3}}{2}\end{matrix}\right.\\m>-\dfrac{3}{2}\\m>-\dfrac{5}{2}\end{matrix}\right.\) \(\Leftrightarrow m>\dfrac{-1+2\sqrt{3}}{2}\)
Mặt khác: \(\dfrac{1}{\sqrt{x_1}}+\dfrac{1}{\sqrt{x_2}}=\dfrac{4}{3}\)
\(\Rightarrow\dfrac{x_1+x_2+2\sqrt{x_1x_2}}{x_1x_2}=\dfrac{16}{9}\) \(\Rightarrow\dfrac{2m+3+2\sqrt{2m+5}}{2m+5}=\dfrac{16}{9}\)
\(\Rightarrow18m+27+18\sqrt{2m+5}=32m+80\)
\(\Leftrightarrow14m-53=18\sqrt{2m+5}\)
\(\Rightarrow\) ...
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2021
\(\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\\Delta'=\left(m+4\right)^2-\left(5m+2\right)\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\-1\le m\le2\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+4\right)}{2m-1}\\x_1x_2=\dfrac{5m+2}{2m-1}\end{matrix}\right.\)
\(x_1^2+x_2^2=2x_1x_2+16\Leftrightarrow\left(x_1+x_2\right)^2=4x_1x_2+16\)
\(\Leftrightarrow4\left(\dfrac{m+4}{2m-1}\right)^2=4\left(\dfrac{5m+2}{2m-1}\right)+16\)
\(\Leftrightarrow-25m^2+25m+14=0\Rightarrow\left[{}\begin{matrix}m=-\dfrac{2}{5}\\m=\dfrac{7}{5}\end{matrix}\right.\) (đều thỏa mãn)
Tớ sửa lại đề 1 chút:
\(x^2-\left(5m-1\right)x+6m^2-2m=0\)
Gọi x1;x2 là các nghiệm của PT. Tìm m để \(x_1^2+x_2^2=1\)
Giải
Theo hệ thức Vi-ét ta có:\(\hept{\begin{cases}x_1+x_2=5m-1\\x_1x_2=6m^2-2m\end{cases}}\)
Do đó: \(x_1^2+x_2^2=1\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=1\)
\(\Leftrightarrow\left(5m-1\right)^2-2\left(6m^2-2m\right)=1\)
\(\Leftrightarrow25m^2-10m+1-12m^2+4m=1\)
\(\Leftrightarrow13m^2-6m=0\)
\(\Leftrightarrow m\left(13m-6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}m=0\\13m-6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}m=0\\m=\frac{6}{13}\end{cases}}}\)
Vậy m=0 hoặc m=\(\frac{6}{13}\)thì phương trình có 2 nghiệm x1;x2 thỏa mãn \(x_1^2+x_2^2=1\)