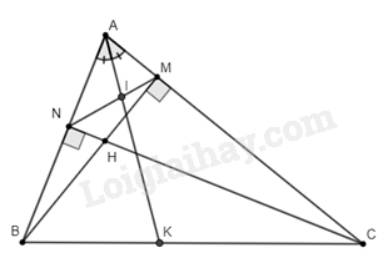
Bài 1.CHo tam giác nhọn ABC có các đường cao AD , BE , CF cắt nhau tại H1. Chứng minh tam giác ABE và tam giác ACF đồng dạngXét \(\Delta ABE\) và \(\Delta ACF\) :\(\widehat{AEB}=\widehat{AFC}\) (\(=90^o\) )\(\widehat{A}\) chung\(\Rightarrow\Delta ABE\sim\Delta ACF\left(g.g\right)\)2.Chứng minh \(\widehat{AEF}=\widehat{ABC}\)Vì tam giác ABE đồng dạng với tam giác ACF ( cmt )\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AE}\)Xét tam giác AEF và tam giác...
Đọc tiếp
Bài 1.CHo tam giác nhọn ABC có các đường cao AD , BE , CF cắt nhau tại H
1. Chứng minh tam giác ABE và tam giác ACF đồng dạng
Xét \(\Delta ABE\) và \(\Delta ACF\) :
\(\widehat{AEB}=\widehat{AFC}\) (\(=90^o\) )
\(\widehat{A}\) chung
\(\Rightarrow\Delta ABE\sim\Delta ACF\left(g.g\right)\)
2.Chứng minh \(\widehat{AEF}=\widehat{ABC}\)
Vì tam giác ABE đồng dạng với tam giác ACF ( cmt )
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AF}{AE}\)
Xét tam giác AEF và tam giác ABC:
\(\widehat{A}\) chung
\(\dfrac{AB}{AC}=\dfrac{AF}{AE}\) (cmt )
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c.g.c\right)\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) ( hai góc t/ứ)
3.Vẽ DM vuông gosc với AC tại M . Gọi K là giao điểm của CH và DM . Chứng minh \(\dfrac{BH}{EH}=\dfrac{DK}{MK}\) và \(AH.AD+CH.CF=\dfrac{CD^4}{CM^2}\)
Bài 2 : Cho ba số \(x,y,z\) khác 0 và \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\) . Tính giá trị của biểu thức \(P=\dfrac{2017}{3}xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)\)