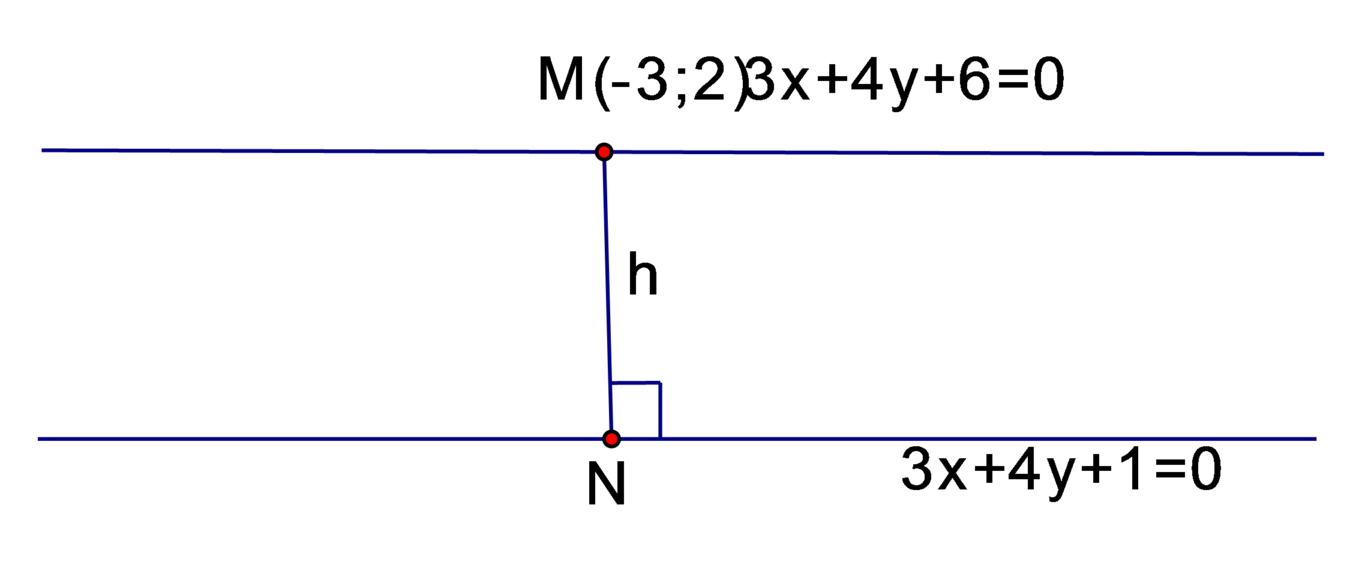
Bài 1: trong hệ trực tọa độ Oxy cho phương trình đường thẳng :3x+4y=2 (d)
a, tìm hệ số của đường thẳng (d)
b, với giá trị nào của m thì đường thẳng (d') : y=(m2-1)x+m song song với đường thẳng (d)
Bài 2 a, trên hệ trực tọa độ Oxy , đường thẳng y+ã+b đi qua 2 điểm M(3;2) và N(4;-1).Tìm hệ số góc a,b
b, trong mặt phẳng tọa độ Oxy , với giá trị nào của a ,b thì đường thẳng (d) : y=ax+2-b và đường thẳng (d') y=(3-a)x+b song song với nhau
Bài 3 Tmf số có hai chữ số biết chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 và số đố gấp 7 lần tổng các chữ sô của nó
GIÚP MÌNH VỚI MAI MÌNH PHẢI NỘP RỒI < ĐANG TRONG DỊCH