1 (2 điểm). Cho hàm số: f(x) = -6x + 9
1) Tính f(0), f(3/2)
2) Tìm x trong các trường hợp f(x) = -9, f(x) = – x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 1:
f(0) => -6.0+9 = 0+9 = 9
f(3/2) => -6.3/2+9 = -18/2 + 9 = (-9) + 9 = 0
Câu 2
f(x) = -9 => -6x+9= -9
-6x = (-9) - 9
-6x = -18
x = (-18) : (-6)
x = 3
* Mình mớ làm được đến thế thôi, bạn nghĩ tiếp nha, hi hi :))

a: \(f\left(x\right)=\sqrt{x^2-6x+9}=\sqrt{\left(x-3\right)^2}=\left|x-3\right|\)
\(f\left(-1\right)=\left|-1-3\right|=4\)
\(f\left(5\right)=\left|5-3\right|=\left|2\right|=2\)
b: f(x)=10
=>\(\left[{}\begin{matrix}x-3=10\\x-3=-10\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=13\\x=-7\end{matrix}\right.\)
c: \(A=\dfrac{f\left(x\right)}{x^2-9}=\dfrac{\left|x-3\right|}{\left(x-3\right)\left(x+3\right)}\)
TH1: x<3 và x<>-3
=>\(A=\dfrac{-\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{-1}{x+3}\)
TH2: x>3
\(A=\dfrac{\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{1}{x+3}\)

Ở góc trái khung soạn thảo có hỗ trợ viết công thức toán (biểu tượng $\sum$). Bạn viết lại đề bằng cách này để được hỗ trợ tốt hơn.

Ta có
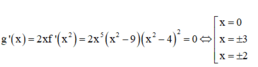
Bảng biến thiên của hàm số y= g( x)
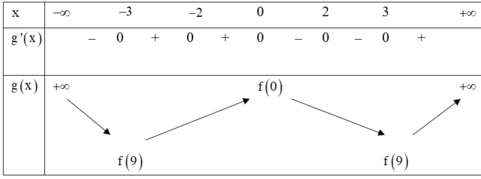
Dựa vào bảng biến thiên ta thấy hàm số đồng biến trên khoảng ( 3: + ∞) hàm số nghịch biến trong khoảng (-∞; -3) .
Hàm số có 3 cực trị, hàm số đạt giá trị nhỏ nhất tại x= ±3
Vậy có 3 khẳng định đúng là khẳng định I, II, IV
Chọn C.

Bài 8:
a) f(-1) = (-1) - 2 = -3
f(0) = 0 - 2 = -2
b) f(x) = 3
\(\Rightarrow x-2=3\)
\(x=3+2\)
\(x=5\)
Vậy \(x=5\) thì f(x) = 3
c) Thay tọa độ điểm A(1; 0) vào hàm số, ta có:
VT = 0; VP = 1 - 2 = -1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm A(1; 0) không thuộc đồ thị của hàm số đã cho
Thay tọa độ điểm B(-1; -3) vào hàm số, ta có:
VT = -3; VP = -1 - 2 = -3
\(\Rightarrow VT=VP=-3\)
\(\Rightarrow\) Điểm B(-1; -3) thuộc đồ thị hàm số đã cho
Thay tọa độ điểm C(3; -1) vào hàm số, ta có:
VT = -1; VP = 3 - 2 = 1
\(\Rightarrow VT\ne VP\)
\(\Rightarrow\) Điểm C(3; -1) không thuộc đồ thị hàm số đã cho.

Câu 5:
a: Khi m=3 thì \(f\left(x\right)=\left(2\cdot3+1\right)x-3=7x-3\)
\(f\left(-3\right)=7\cdot\left(-3\right)-3=-21-3=-24\)
\(f\left(0\right)=7\cdot0-3=-3\)
b: Thay x=2 và y=3 vào f(x)=(2m+1)x-3, ta được:
\(2\left(2m+1\right)-3=3\)
=>2(2m+1)=6
=>2m+1=3
=>2m=2
=>m=1
c: Thay m=1 vào hàm số, ta được:
\(y=\left(2\cdot1+1\right)x-3=3x-3\)
*Vẽ đồ thị
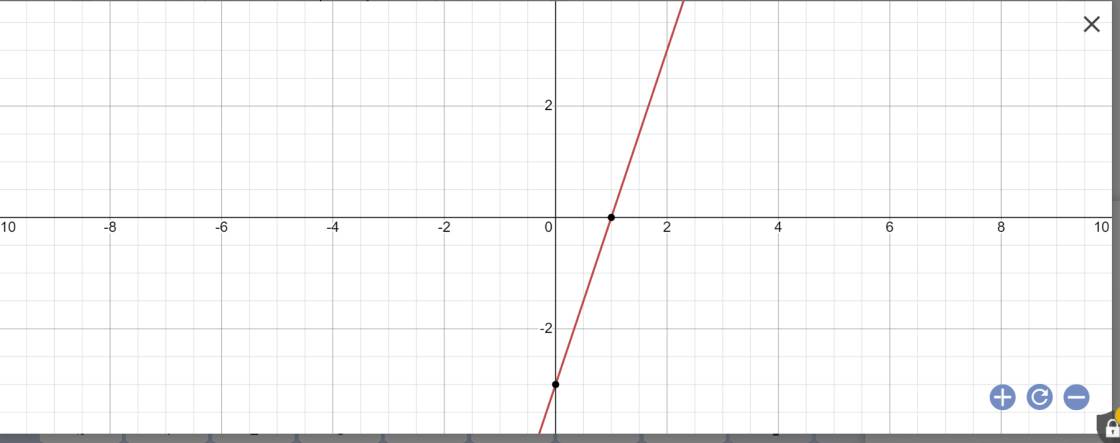
d: Để hàm số y=(2m+1)x-3 là hàm số bậc nhất thì \(2m+1\ne0\)
=>\(2m\ne-1\)
=>\(m\ne-\dfrac{1}{2}\)
e: Để đồ thị hàm số y=(2m+1)x-3 song song với đường thẳng y=5x+1 thì \(\left\{{}\begin{matrix}2m+1=5\\-3\ne1\end{matrix}\right.\)
=>2m+1=5
=>2m=4
=>m=2

a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3
g(-1) = 0,5; g(-2) = 2; g(0) = 0
b) f(x) = 2 ⇒ x = 1
g(x) = 2 ⇒ x = 2 hoặc x = -2
1) - Thay x = 0 vào hàm số f(x) ta được :
\(f_{\left(0\right)}=-6.0+9=0\)
- Thay x = \(\frac{3}{2}\) vào hàm số f(x) ta được :
\(f_{\left(\frac{3}{2}\right)}=-6.\frac{3}{2}+9=0\)
2) - Thay \(f_{\left(x\right)}=-9\) vào hàm số trên ta được :
\(-6x+9=-9\)
=> \(-6x=-18\)
=> \(x=3\)
Vậy với f(x) = -9 thì x = 3 .
- Thay \(f_{\left(x\right)}=-x2\) vào hàm số trên ta được :
\(-6x+9=-x2\)
=> \(-4x=-9\)
=> \(x=\frac{9}{4}\)
Vậy với f(x) = -2x thì x = \(\frac{9}{4}\) .
1) f(0)= -6 . 0 +9 =9
f(3/2)=\(-6\cdot\frac{3}{2}+9=0\)
2) f(x)=-9 <=> -6x+9=-9 <=> -6x=-18 <=> x=3
\(f\left(x\right)=-x^2\\ \Leftrightarrow -6x+9=-x^2\\ \Leftrightarrow x^2-6x+9=0\\ \Leftrightarrow\left(x-3\right)^2=0\Leftrightarrow x-3=0\Leftrightarrow x=3\)