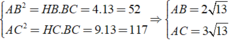cho tam giác ABC vuông tại A có đường cao AH chia cạnh BC thành hai đoạn thẳng HB=4cm , HC=9cm . vẽ (A;AH), vẽ hai tiếp tuyến BM ,CN với đường tròn (M,N là các tiếp điểm khác H)
a. tính AH,AB
B. gọi I là giao điểm của AB và HM , K là giao điểm của AC và HN . tứ giác AIHK là hình gì ? vì sao ?
C. CMR: BC là tiếp tuyến của đường tròn đường kính MN