Tính giá trị của biểu thức\(A=\left(x-3\right)\left(x^2+3x+9\right)-x\left(x^2-3\right)\)tại x=9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 12 2018
a,ĐK: \(\hept{\begin{cases}x\ne0\\x\ne\pm3\end{cases}}\)
b, \(A=\left(\frac{9}{x\left(x-3\right)\left(x+3\right)}+\frac{1}{x+3}\right):\left(\frac{x-3}{x\left(x+3\right)}-\frac{x}{3\left(x+3\right)}\right)\)
\(=\frac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\frac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)
\(=\frac{x^2-3x+9}{x\left(x-3\right)\left(x+3\right)}.\frac{3x\left(x+3\right)}{-x^2+3x-9}=\frac{-3}{x-3}\)
c, Với x = 4 thỏa mãn ĐKXĐ thì
\(A=\frac{-3}{4-3}=-3\)
d, \(A\in Z\Rightarrow-3⋮\left(x-3\right)\)
\(\Rightarrow x-3\inƯ\left(-3\right)=\left\{-3;-1;1;3\right\}\Rightarrow x\in\left\{0;2;4;6\right\}\)
Mà \(x\ne0\Rightarrow x\in\left\{2;4;6\right\}\)
23 tháng 9 2021
\(x=\dfrac{\sqrt[3]{\left(2+\sqrt{3}\right)^3}\left(2-\sqrt{3}\right)}{\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}}=\dfrac{1}{\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}}\)
Đặt \(A=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)\(\Leftrightarrow A^3=18+3\sqrt[3]{\left(9-4\sqrt{5}\right)\left(9+4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\\ \Leftrightarrow A^3=18+3A\sqrt[3]{1}\\ \Leftrightarrow A^3-3A-18=0\\ \Leftrightarrow A=3\\ \Leftrightarrow X=\dfrac{1}{3}\\ \Leftrightarrow Q=\left[3\left(\dfrac{1}{3}\right)^3-\left(\dfrac{1}{3}\right)^2-1\right]^{2021}=\left(\dfrac{1}{9}-\dfrac{1}{9}-1\right)^{2021}=\left(-1\right)^{2021}=-1\)
22 tháng 7 2023
`a, = 3x^2y - 3xy + 6x^2y + 5xy - 9x^2y`
`= 2xy`.
Thay `x = 2/3; y = -3/4` vào BT:
`2 . 2/3 . -3/4 = -1.`
`b, x(x-2y) - y(y^2-2x)`
`= x^2 - 2xy - y^3 + 2xy`
`= x^2 - y^3`
Thay `x = 5; y =3` vào BT:
`= 5^2 - 3^3 = 25 - 27 = -2`
H9
HT.Phong (9A5)
CTVHS
22 tháng 7 2023
a) \(3x^2y-\left(3xy-6x^2y\right)+\left(5xy-9x^2y\right)\)
\(=3x^2y-3xy+6x^2y+5xy-9x^2y\)
\(=2xy\)
Thay \(x=\dfrac{2}{3},y=-\dfrac{3}{4}\) vào Bt ta có:
\(2\cdot\dfrac{2}{3}\cdot-\dfrac{3}{4}=-1\)
b) \(x\left(x-2y\right)-y\left(y^2-2x\right)\)
\(=x^2-2xy-y^3+2xy\)
\(=x^2-y^3\)
Thay \(x=5,y=3\) vào Bt ta có:
\(5^2-3^3=-3\)
16 tháng 9 2021
a: Ta có: \(A=\left(\dfrac{3x+3}{x-9}-\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\left(\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right)\)
\(=\dfrac{3x+3-2x+6\sqrt{x}-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}-3}{2\sqrt{x}-2-\sqrt{x}+3}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
14 tháng 8 2016
Ta có :
\(\left(x+3\right)^3-\left(x+9\right)\left(x^2+27\right)\)
\(=x^3+9x^2+27x+27-\left[x^3+27x+9x^2+243\right]\)
\(=27-9.27\)
\(=8.27=216\)
DO đó ...
20 tháng 7 2018
a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3\left(x^2-2x+1\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của x.
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+4x^2+4x+1+x^3+27-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
\(=27\)
Vậy ...
H9
HT.Phong (9A5)
CTVHS
24 tháng 6 2023
1, \(A=5x\left(x^2-3\right)+x^2\left(7-5x\right)-7x^2\)
\(A=5x^3-15x+7x^2-5x^3-7x^2\)
\(A=\left(5x^3-5x^3\right)+\left(7x^2-7x^2\right)-15x\)
\(A=-15x\)
Thay \(x=-5\) vào A ta được:
\(-15\cdot-5=75\)
Vậy: ....
2. \(B=x\left(x^2-3\right)+x^2\left(7-5x\right)-7x^2\)
\(B=x^3-3x+7x^2-5x^3-7x^2\)
\(B=\left(x^3-5x^3\right)+\left(7x^2-7x^2\right)-3x\)
\(B=-4x^3-3x\)
Thay \(x=10,y=-1\) vào B ta được:
\(-4\cdot10^3-3\cdot10=-4\cdot1000-3\cdot10=-4000-30=-4030\)
Vậy: ....
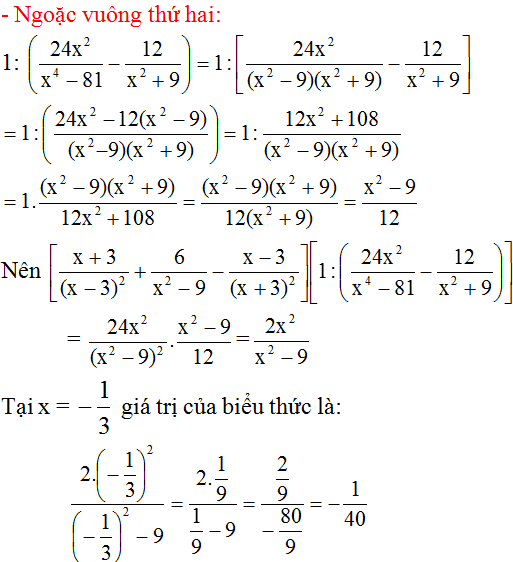
A = (9 - 3)(92 + 3.9 + 9) - 9.(92 - 3)
= 6.117 - 702
= 0
Rút gọn thế được chưa