Cho tam giác MBC vuông tại M(MB<MC) . Kẻ đường phân giác BD của tam giác (D thuộc MC).Qua D kẻ đường thẳng vuông góc với B tại A, MA cắt BD tại H
a,Chứng minh tam giác BMD= tam giác BAD
b,Chứng minh BD là đường trung trức của đoạn thẳng MA
c,Qua A kẻ đường thẳng song song với với BD cắt MB ở E và cắt MC ở F .Chứng minh EF vuông góc với MA và tam giác DÀ là tam giác cân
d,Chứng minh B là trung điểm của ME.


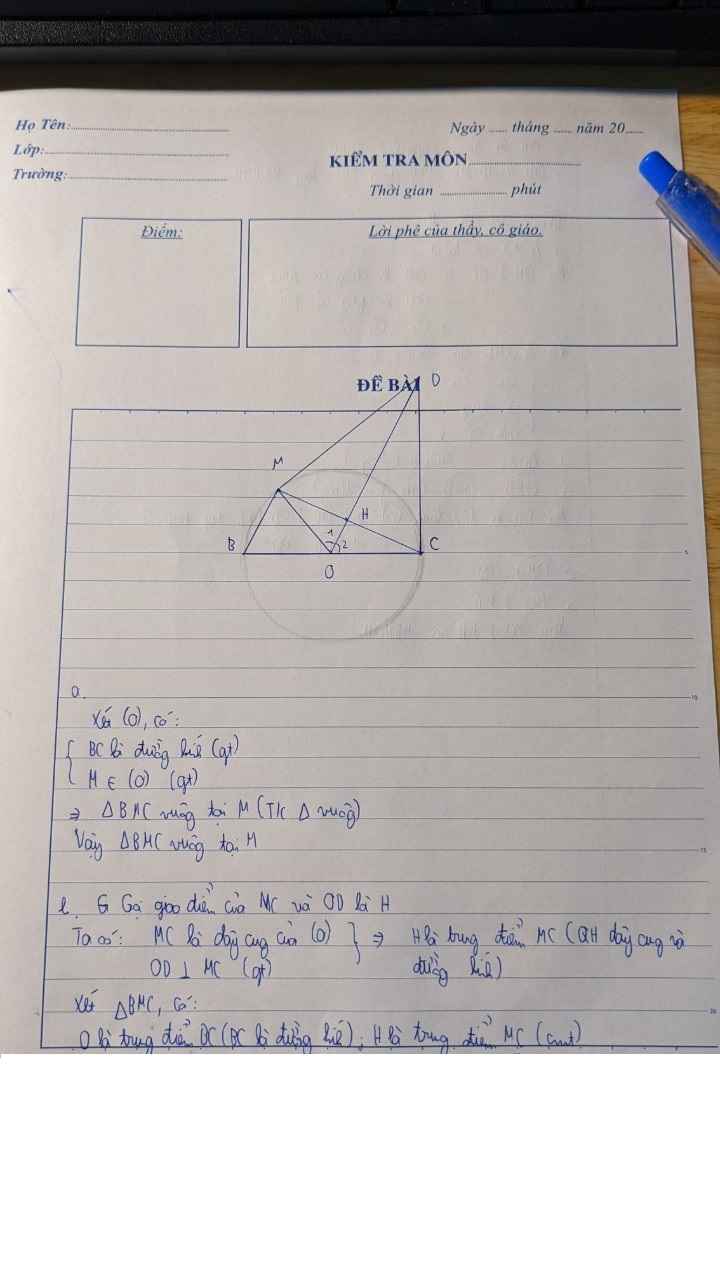

Gọi D,F lần lượt là trung điểm của AB,AC chứng minh tam giác DFH cân