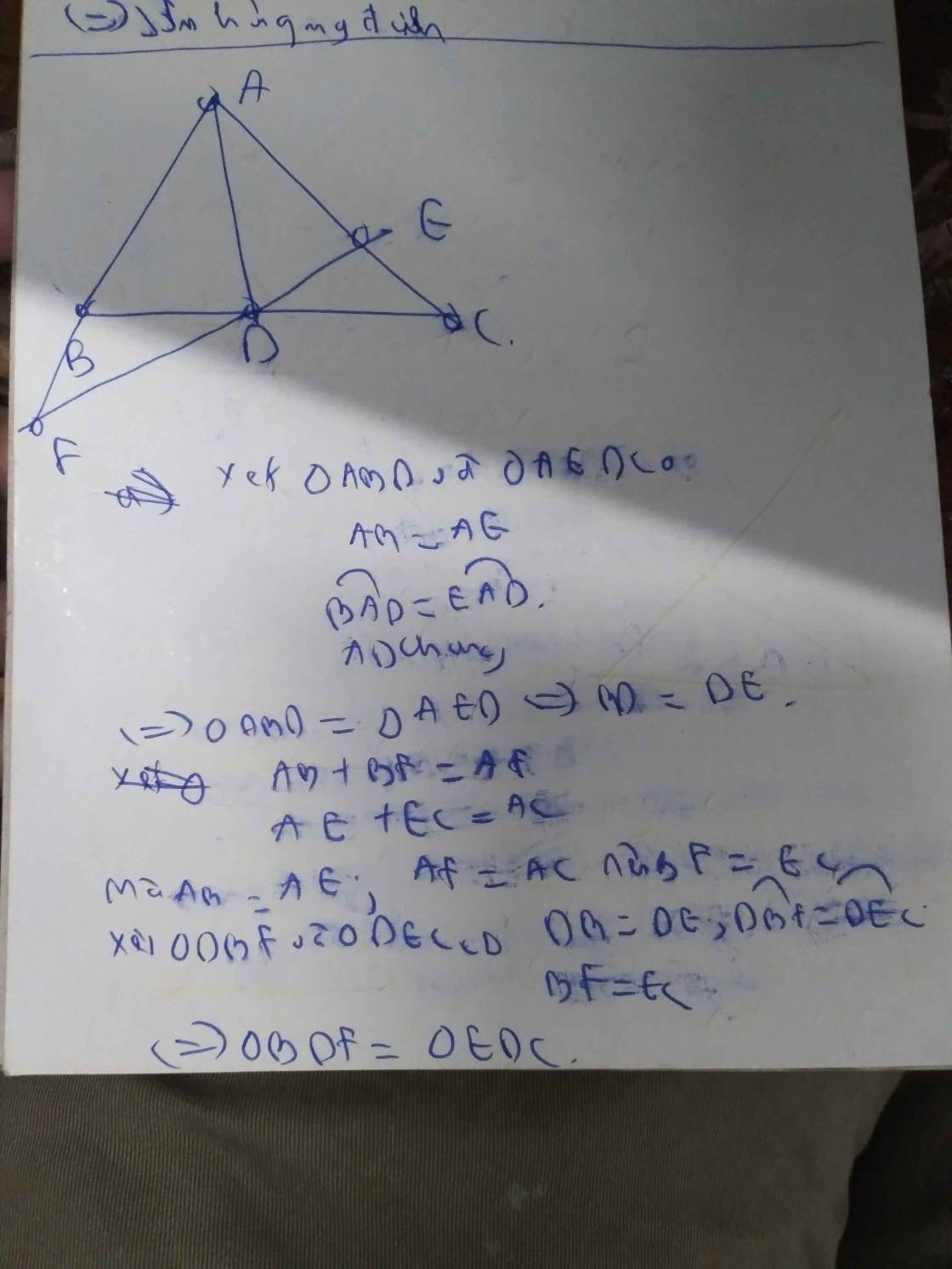
Cho tam giác ABC có AB > AC.Trên AB lấy F sao cho AC = AF, gọi AD là tia phân giác của góc BAC trên lấy E tùy ý.1,Chứng minh AB - AC = EF;2,chứng minh BE - EC < BF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔADF và ΔADC có
AD chung
\(\widehat{FAD}=\widehat{CAD}\)
AF=AC
Do đó: ΔADF=ΔADC
b: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE và \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{CED}\)
Ta có: AB+BF=AF
AE+EC=AC
mà AB=AE và AF=AC
nên BF=EC
Xét ΔDBF và ΔDEC có
DB=DE
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
Do đó: ΔDBF=ΔDEC
=>\(\widehat{BDF}=\widehat{EDC}\)
mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)
nên \(\widehat{BDE}+\widehat{BDF}=180^0\)
=>E,D,F thẳng hàng
c: Ta có: ΔDBF=ΔDEC
=>DF=DC
=>D nằm trên đường trung trực của CF(1)
ta có: AF=AC
=>A nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra AD là đường trung trực của CF
=>AD\(\perp\)CF

a:
AB+BF=AF
AE+EC=AC
mà AB=AE và AC=AF
nên BF=EC
Xét ΔAEF và ΔABC có
AE=AB
\(\widehat{EAF}\) chung
AF=AC
Do đó: ΔAEF=ΔABC
=>\(\widehat{AEF}=\widehat{ABC}\) và \(\widehat{AFE}=\widehat{ACB}\)
\(\widehat{ABD}+\widehat{FBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{DEC}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)
nên \(\widehat{FBD}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
BF=EC
\(\widehat{DFB}=\widehat{DCE}\)
Do đó: ΔDBF=ΔDEC
=>DB=DE
Xét ΔABD và ΔAED có
AB=AE
BD=ED
AD chung
Do đó: ΔABD=ΔAED
=>\(\widehat{BAD}=\widehat{EAD}\)
=>AD là phân giác của \(\widehat{BAC}\)
b: Xét ΔABM và ΔAEM có
AB=AE
\(\widehat{BAM}=\widehat{EAM}\)
AM chung
Do đó: ΔABM=ΔAEM
=>MB=ME
AC-AB=EC
mà EC>MC-ME
và MC=MF
nên AC-AB>MC-ME=MC-MB(ĐPCM)

Cho tam giác ABC, AB<AC.Tia p/g của góc A cắt BC ở D, trên tia AC lấy điểm E sao cho AE=AB. Gọi tia M là giao điểm của AB va DE
Cmr: a) tam giác ABD=tam giacd AED
b) tam giacd DBM=tam giác DEC

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra: DB=DE và \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBF}=\widehat{DEC}\)
Xét ΔDBF và ΔDEC có
\(\widehat{DBF}=\widehat{DEC}\)
DB=DE
\(\widehat{BDF}=\widehat{EDC}\)
Do đó: ΔDBF=ΔDEC

a) Mk nghĩ bn cheps sai đề bài rùi!!! Phải là c/m: tam giác ABD = tam giác ACD chứ!!
Xét \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (gt)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{A}\))
AD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c.g.c\right)\)
b) Mk nghĩ bn lại sai đề bài!!! Làm sao c/m đc EF = AD??!!!! Đáng lẽ ra phải là EF = BD ms đúng chứ!!!!
Xét \(\Delta AEF\)và \(\Delta ADB\)có:
AE = AD (gt)
\(\widehat{EAF}=\widehat{DAB}\)(2 góc đối đỉnh)
AF = AB (gt)
\(\Rightarrow\Delta AEF=\Delta ADB\left(c.g.c\right)\)
=> EF = DB (2 cạnh tương ứng)
c) Ta có: AF = AB, mà AC = AB
=> AF = AC
Xét \(\Delta AHF\)và \(\Delta AHC\)có:
AF = AC (cmt)
AH là cạnh chung
HF = HC (H là trung điểm của FC)
\(\Rightarrow\Delta AHF=\Delta AHC\left(c.c.c\right)\)
\(\Rightarrow\widehat{FAH}=\widehat{CAH}\)(2 góc tương ứng)
=> AH là tia phân giác của \(\widehat{CAF}\)
d)